量子コンピューティング
量子スピン鎖の大規模シミュレーションを行う量子アルゴリズム
2024-11-18
カテゴリー IBM Research (コンピューティング) | 量子コンピューティング
記事をシェアする:
Stony Brook大学の研究者は、計算能力の限界を押し進めて実用規模のスピン鎖シミュレーションを可能にするために、さまざまな量子シミュレーション手法を組み合わせて改良しています。
量子計算の起こりがいつかというと、多くの人が、物理学者のリチャード・ファインマンが「自然現象をシミュレーションしたいなら、量子力学的な方法を用いるべきだ」と宣言した1981年であると考えています。40年近くが経った現在も、量子シミュレーションは量子コンピューターの最も有望なアプリケーションの 1つですが、当時と違うのは、私たちは今や実用規模の量子ハードウェアを手にしているということです。これを用いれば、古典手法では実用が難しい量子シミュレーションを、100量子ビット以上を用いて十分な高精度で実行することができます。
研究者たちは、量子コンピューターが最終的には、古典的な方法を完全に超えた量子系のシミュレーションを可能にすることを期待しています。 そのためには量子ハードウェアだけでなく、量子アルゴリズムも改善し、ノイズによって引き起こされるエラーに打ち勝たなければなりません。 量子コンピューターが潜在能力を最大限に発揮するためには、研究者が実用規模の量子ハードウェアを使用して、大規模なシミュレーション実験を実行し、有用な量子アルゴリズムの開発を継続することが重要です。これには、新しい量子アルゴリズムを考案することと、既存の方法を結合して改良する方法を見つけることの両方が含まれます。いずれの場合にも、目標は、今日利用可能な実用規模のデバイスを最大限に活用できて、また、将来のより強力な量子プロセッサーにも拡張可能なアルゴリズムを構築することです。
このブログ投稿でご紹介するのは、ニューヨークにある Stony Brook大学の研究者による、まさにその点で重要な研究です。この研究で彼らは、IBMの超伝導量子コンピューター上で、最大 102量子ビットを用いて実装した変分量子アルゴリズムを使用して、興味深い量子系のシミュレーション結果を示しました。この研究は昨年の Physical Review Researchに掲載されました。Stony Brook大学の研究チームの実験は、比較的に深さの浅い量子回路を用いているため、古典コンピューター上での愚直なシミュレーションでも実行可能な規模ではありますが、変分量子アルゴリズムの大規模実装に向けた重要な進展であります。変分量子アルゴリズムは、量子シミュレーション研究でいま広く研究されています。
以下では、量子系の正確な基底状態エネルギーを量子コンピューターを使って求めるのに著者たちが使用した手法のキーポイントについて説明します。特に、物理的な意味を裏付けとして持ったアンザッツと、エネルギー測定実験の実行に使用した実験手順、そしてエラー緩和のアプローチについて詳しく説明します。
物理的な根拠に基づいた、スピン鎖シミュレーションのためのアンザッツ
この研究で著者たちは XXZ と ハイゼンベルグ・スピン鎖という 2つの単純化された磁性モデルに焦点を当てました。スピン鎖は、「スピン」を持った粒子からなる系としてイメージすることができます。「固有の回転モーメント」を持った粒子がすべて格子状に並べられた状態で、それは、異なる種類の材料を形成するように粒子が並んでいるのと同じ様子です。
これらのスピン鎖の中のスピンがどのように振る舞って相互作用するかを分析することにより、物理学者は、量子系内の物質の量子相について多くのことを学ぶことができます。 物質の量子状態は、もっとよく知られている液体や気体といった物質の状態に似ています。 物理学者は、物質の量子相と、さらには一つの量子相から別の相へどのように転移するかを研究します。これは、化学者が液体の水がどのようにして水蒸気に変化するかを研究する方法と似ています。
Stony Brook大学の研究者は、量子ハードウェア上で大規模なスピン鎖系をシミュレーションして、それらの系の基底状態エネルギーを求めることを目標としました。 基底状態エネルギーとは、励起状態ではなく平衡状態にある量子系のエネルギーのことで、それはシステムが持ちうる最低のエネルギー状態です。
【注】XXZスピン鎖と ハイゼンベルグ・スピン鎖
XXZモデルや ハイゼンベルグ・モデルとは、量子スピン鎖と呼ばれる、磁性や他の量子力学系における粒子のスピン効果を研究するために使用される物理モデルです。量子力学では、「スピン」は粒子固有の特性です。 量子スピン・モデルは、数値アルゴリズムのテストベッドとして、また、量子「相」と呼ばれる物質の状態を理解するための有用なツールとして頻繁に使用されます。
XXZスピン鎖や ハイゼンベルグ・スピン鎖は、1次元上に、つまり線の上に並べられた粒子の格子と考えることができます。これらのモデルは最近傍の相互干渉のみを想定します。ということは、格子上のある場所にあるスピンは、両隣のスピンとのみ相互作用をします。
XXZモデルは異なる複数の相を持つことが知られています。 1つは強磁性相です。 系が強磁性相にある時 すべてのスピンは同じ方向に揃いますが、反強磁性相にある時は反対方向を向きます。強磁性材料でこの方向が揃った状態は、その物質の最低エネルギー状態を表します。それに対して、どんな方向に向かってでもいいですがスピンが傾いた状態になっていると、系のエネルギーが変化します。このことは「自発的対称性の破れ」と呼ばれます。
この論文で検討されているハイゼンベルク鎖は、XXZモデルの一つの特殊なケースで、鎖が、すべての方向に同じ強度の(つまり等方性の)反強磁性相互作用を持った状態です。反強磁性に向かう傾向を持ってはいますが、ハイゼンベルクのモデルの基底状態は依然として反強磁性秩序は示しません。すなわち、スピン回転対称性を示します。
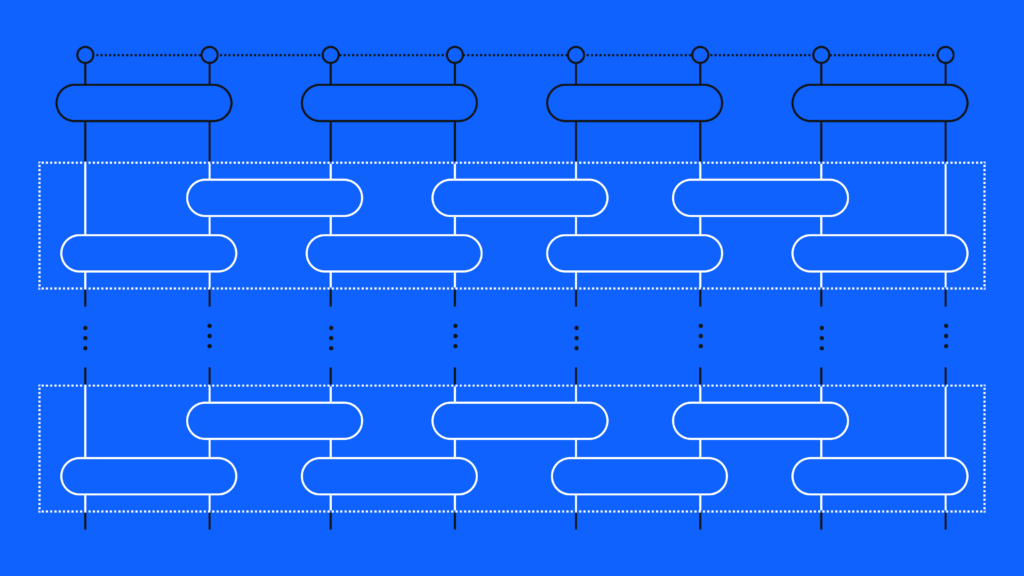
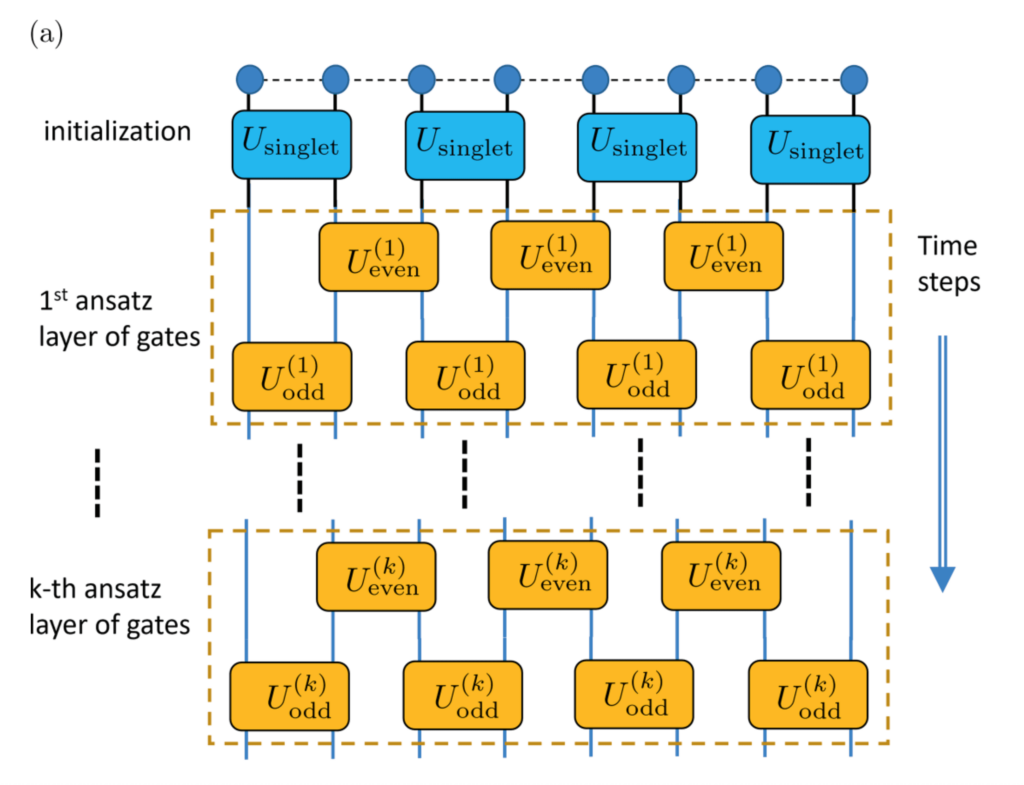
著者たちは、XXZモデルとハイゼンベルク・モデルの物理学に基づいたアンザッツを実装して実験を開始しました。量子計算では、アンザッツは、量子系をシミュレーションするために使われる変分量子アルゴリズムで最初に実行される、パラメーター付き量子回路です。 アンザッツは、特定の量子系をシミュレートするための最適な回路と回路パラメーターを、経験に基づいて推測したものであり、「物理的な根拠に基づいたアンザッツ」は、既知の物理理論に基づいて設計されているアンザッツ回路のことです。 変分アルゴリズムは反復型であるため、最初のアンザッツ回路を実行すると、アルゴリズムは、最初の回路実行から得られた出力を使用して、回路パラメーターを最適化してから、再び同じ回路を実行します。 この反復サイクルは、アルゴリズムが最適な出力に達するまで続きます。
Stony Brook大学の研究者は、まずXXZモデルの合計エネルギーを表すハミルトニアン Hxxz から始めて、そのアンザッツを設計しました。著者らは次にスピン鎖の中の奇数番目(つまり最初のビット、3番目のビットなど)のスピンとその隣接するスピンとの間の相互作用に対応するハミルトニアン項を抽出しました。Hodd と呼ばれるこの新しいハミルトニアンは、既知の基底状態 |Ψsinglet⟩ を持っています。
【注】ハミルトニアン
モデルのハミルトニアンは、その合計エネルギーの数学的記述です。 XXZモデルの場合、隣接するスピン間の異なる相互作用を表す項を合計したものになります。 量子力学では、各ハミルトニアンは異なるひとつのエネルギースペクトルに対応し、それは系全体が持ちうる合計エネルギーの集合を表します。最も低いエネルギーを持つ状態は「基底状態」と呼ばれ、それ以外の状態は「励起状態」と呼ばれます。系の基底状態の特性を理解することは重要ですが、それは系が十分に低い温度でどのように振る舞うかを、基底状態の性質から推論できるからです。
そこから、著者たちは、新しいパラメーター付きハミルトニアン H(s) = (1-s) Hodd + s Hxxz を定義しました。これは、 Hodd と Hxxz の間の線形補間になっています。H(s) の s=0 (すなわち |Ψsinglet⟩) の基底状態から始めて、量子状態の時間発展のステップに対応するパラメーターである s を増加させながら基底状態にとどまることができれば、目的の結果である Hxxz の基底状態に s=1 において到達すると考えられます。
このような物理的直観に着想を得たアンザッツを設計することができます。そのアンザッツは、適切な量子論理ゲートを使用して |Ψsinglet⟩ を実装することで始まります。その後、系はそのハミルトニアン H(s) の項に従って時間発展し、徐々に値 s=1 に向かって sの値を増加させます。この時間発展の間に、(経路中にエネルギーギャップが存在するとして)s=0 のときと同様に系を基底状態に留めることができれば、s が 1 に達した時に Hxxz の基底状態エネルギーが得られます。
このアイデアをゲートを利用したパラメーター付き量子回路として実装するために、著者はトロッター化(Trotterization)と呼ばれる近似を使用してハミルトニアンを離散化しました。 さらに、この離散化された時間発展を、より柔軟性を持った変分形式に変換しました。
これは、この量子回路に使用される多くの量子ゲートがパラメーターで制御可能で、測定されるエネルギーを最小化するようにパラメーターの値を調整することができるということです。また、量子ゲートのパラメータの値(角度)をトロッター化に用いた角度から変更できるようにしたことで、本来トロッター化で生じる近似誤差を補正できる可能性が生じます。
測定手順とエラー緩和
目的の量子状態に到達すると、著者たちは、隣接する量子ビットにベル状態測定を用いて、そのエネルギーを評価しました。 ベル状態測定は、2量子ビットの量子状態を同時に測定します。量子ビットは0または1の状態でしか測定できないため、量子コンピューターで実装されたベル状態測定には、4つの可能な計算結果しかありません。つまり、 |00⟩、 |01⟩、 |10⟩、または |11⟩です。
XXZモデルでは、これら 4つの ベル状態それぞれに特定のエネルギーがあります。 2つの隣接する量子ビット間の結合のエネルギー寄与は、測定結果から得られる ベル状態のエネルギーに対応します。 すべてのエネルギー寄与の合計は、合計エネルギーに対応します。
著者たちはすべての結合を2グループに分割し、各グループ内で並行してベル測定を実行しました。 こうすることで、2セットのベル測定を実行するだけで済みました。
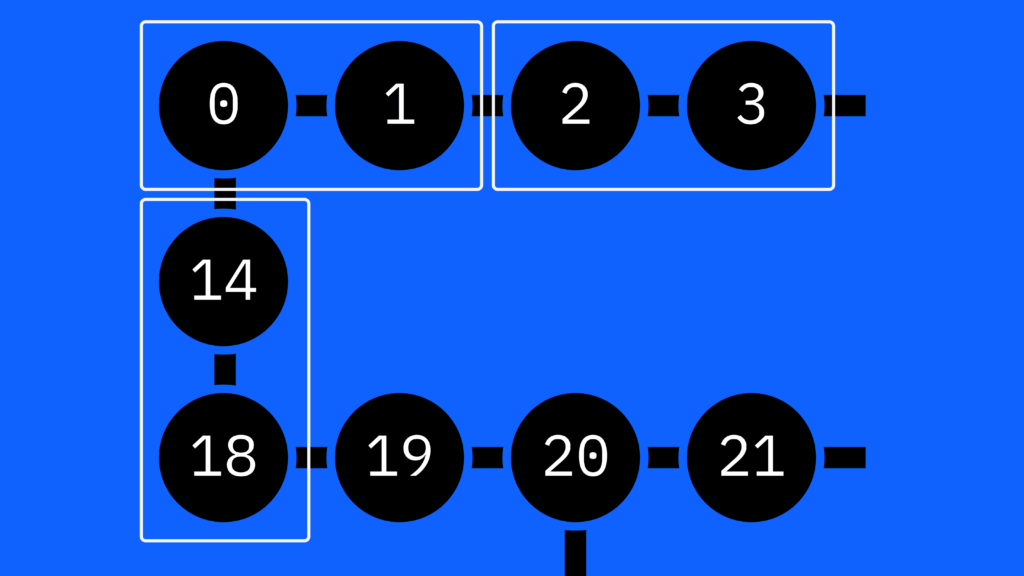
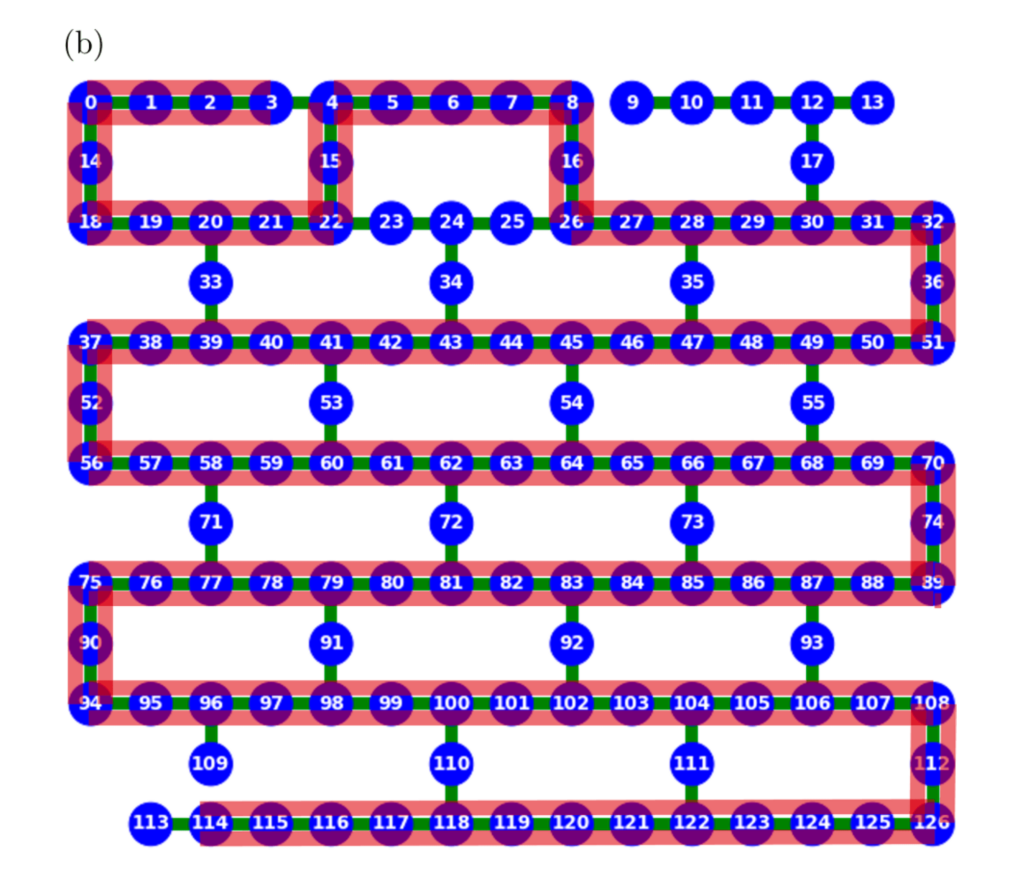
量子チップでは、すべての量子ビットが互いに接続されているわけではありません。個々の量子ビットは「最近傍量子ビット」に接続されています。この画像内の白い長方形は、隣接する接続された量子ビットのペアである「最近傍量子ビット」の例を示しています。 著者たちは、考えられるすべてのペアを測定するために 2セットの測定を実行しました。この図に示されているペアは、2セットのうちの一方の一部として見ることができます。 もう一方のセットには、ペア 2/1、0/14 などが含まれます。
もちろん、これらの測定の出力はノイズによって引き起こされるエラーを含みます。 したがって、測定の後には、エラー緩和が次のステップになります。
著者たちはまず、標準的な読み出しエラー緩和をこのケースに適用することから始めました。XXZモデルは最近傍の相互作用のみを含んでいるため、著者たちは、結合している量子ビットの各ペアの測定の緩和に焦点を当てました。確率行列 Mは本質的には、量子ハードウェアで実行した時に量子アルゴリズムが正しい結果を出力するか誤った結果を出力するかの確率を表現しているので、ここに注目することで M は 4 × 4 の次元を持つことになり、相互作用するハミルトニアンに含まれる量子ビットの各ペアで計算できるようになります。
【注】読み出しエラー緩和
量子ビット数が少ない量子回路の場合、理想の出力確率分布 Pideal を計算して、次に実際の量子ハードウェアである程度の量の測定を実行して、実験的な確率分布 Pmeasured を取得したら、これらの量は確率行列Mを用いて Pmeasured = M*Pideal の式によって関連付けられます。 この関係を逆に利用することで、Mを使って量子デバイスのノイズによる結果を緩和できます。 しかし、N量子ビットに対して、Mのサイズは 2N x 2N となり、量子ビット数が大きい場合にはこのアプローチは使えません。

2量子ビットの Pmeasured = M*Pideal 表現。ここで、Mは 4 × 4 の行列であり、各要素 Pr(a’b’|ab) は、ノイズのあるデバイスで真の状態 |ab⟩ でなく状態 |a’b’⟩ を測定する確率です。緑色で強調表示された対角成分は、ベル測定で正しい結果を観測する確率を表し、赤色の強調表示された残りの部分は、誤った状態を観測する確率を表します。
この手法は、ベル状態測定を扱う場合に特に役立ちます。なぜなら、ベル状態測定には、ノイズの原因となる追加の CNOTゲートが含まれるからです。 上記の手法を使用すると、これらの不完全な CNOTゲートによって発生するノイズと、最終測定によって発生する標準的なノイズの両方を緩和することができます。
変分回路から計算されたエネルギーは、量子ゲート・エラーの影響を受けます。 このエラーを軽減するために、著者たちはゲート・レベルの Zero-noise extrapolation (ZNE) を使用しました。そしてさらに、彼らはそれ以上の工夫を行いました。
【注】Zero-noise extrapolation (ZNE)
ZNEは、以下の考えに基づいています。初期状態 |00…0⟩ に対して理想的な量子回路 U を適用すると、|Ψ⟩ = U|00…0⟩ になります。この状態はさらに、非負整数の値 n について、|Ψn⟩ = U(U-1 U)n |00…0⟩ となります。 量子状態 |Ψ⟩ のオブザーバブル O の期待値である ⟨Ψ| O | Ψ⟩ を評価するときには、異なる nの値に対して同様の結果を得る必要があります。 残念ながら、ノイズは量子ゲートに影響を与え、量子回路の出力にも影響を与えます。 このため nを増やすと、ノイズの量も増加します。 ここでノイズ・レベル m = 1 + 2n を定義しておきます。特に n = 0 は初期状態 |00…0⟩ に適用された U に対応します。したがって、ノイズ・レベルは 1 です。 変分回路 U (とその逆変換である U-1)のゲートを反復するだけで 異なる nの値に対するエネルギーを計算することができるので、異なるレベルのノイズに対して異なる値のエネルギーを求めることができます。これでこのデータを使用して、ゼロ・ノイズ極限 m = 0 における期待値を外挿で求めることができます。
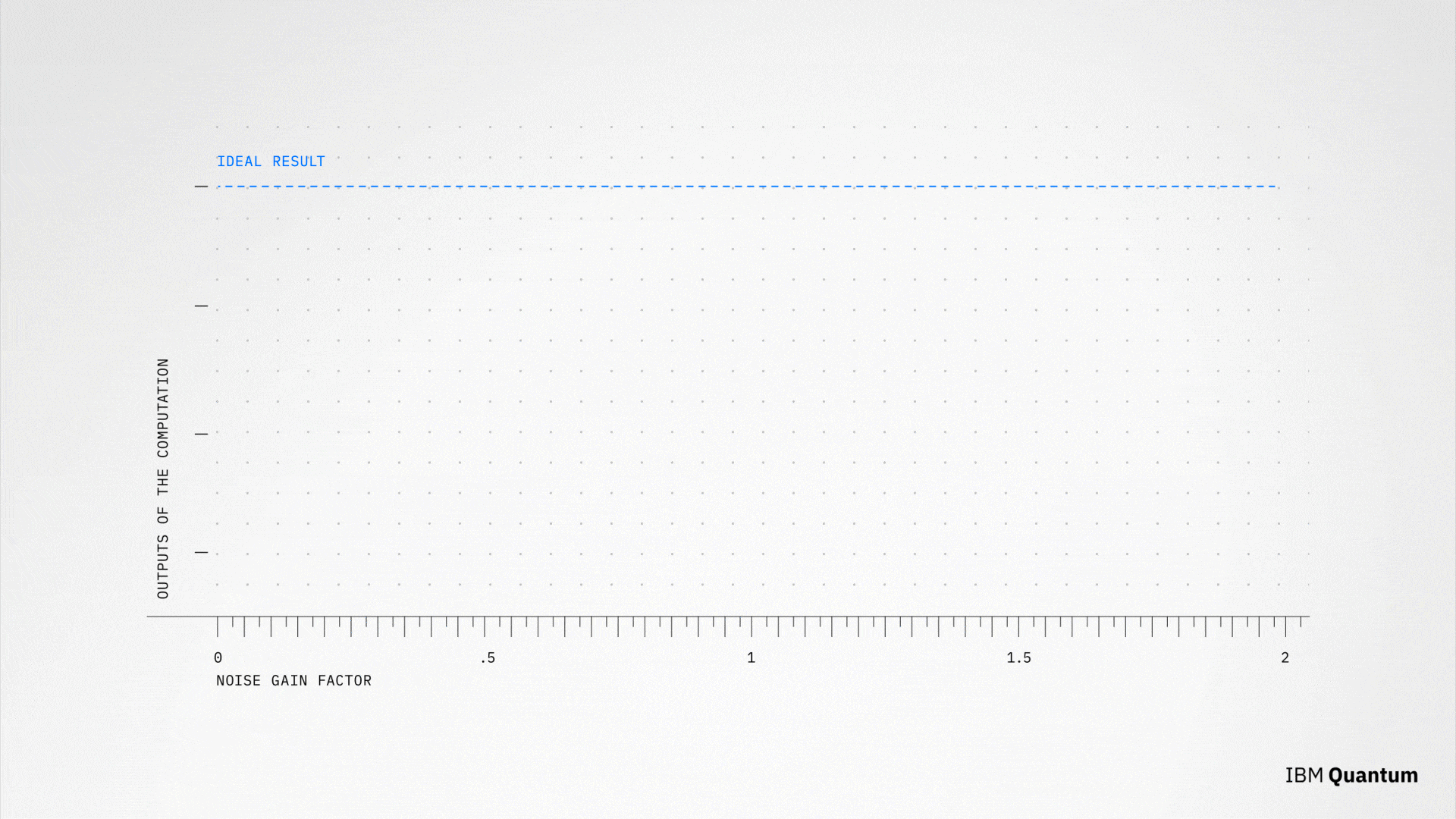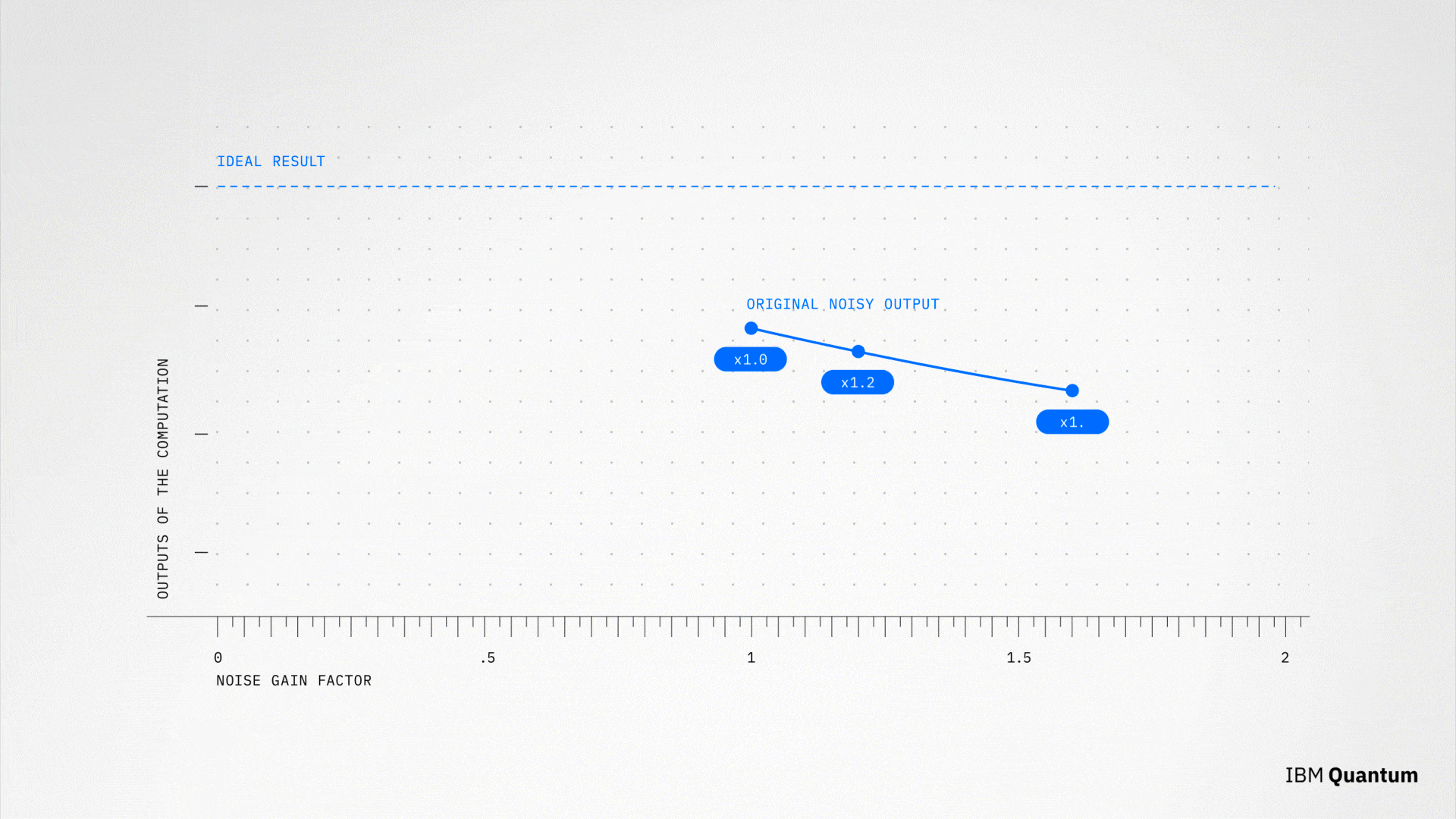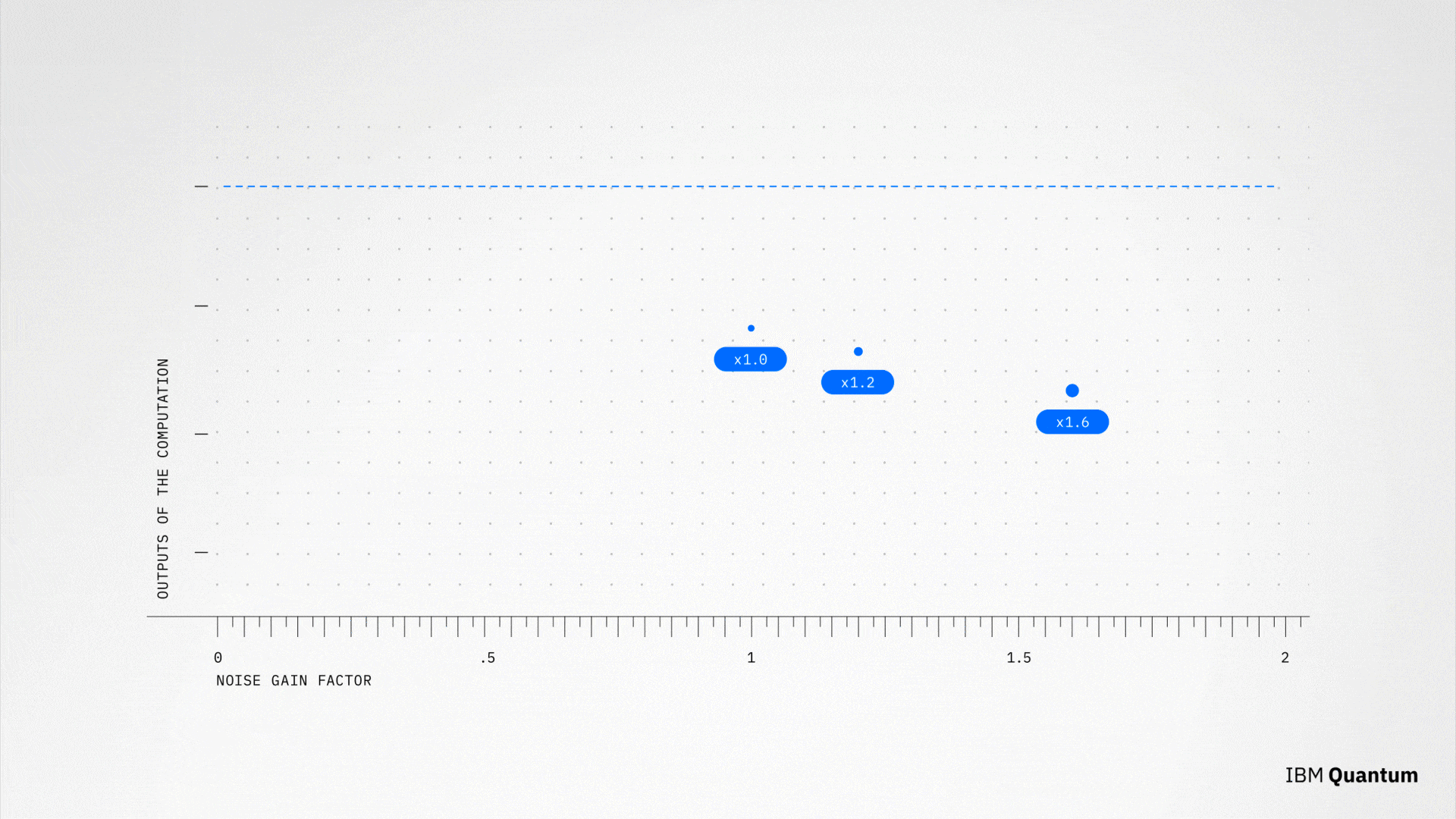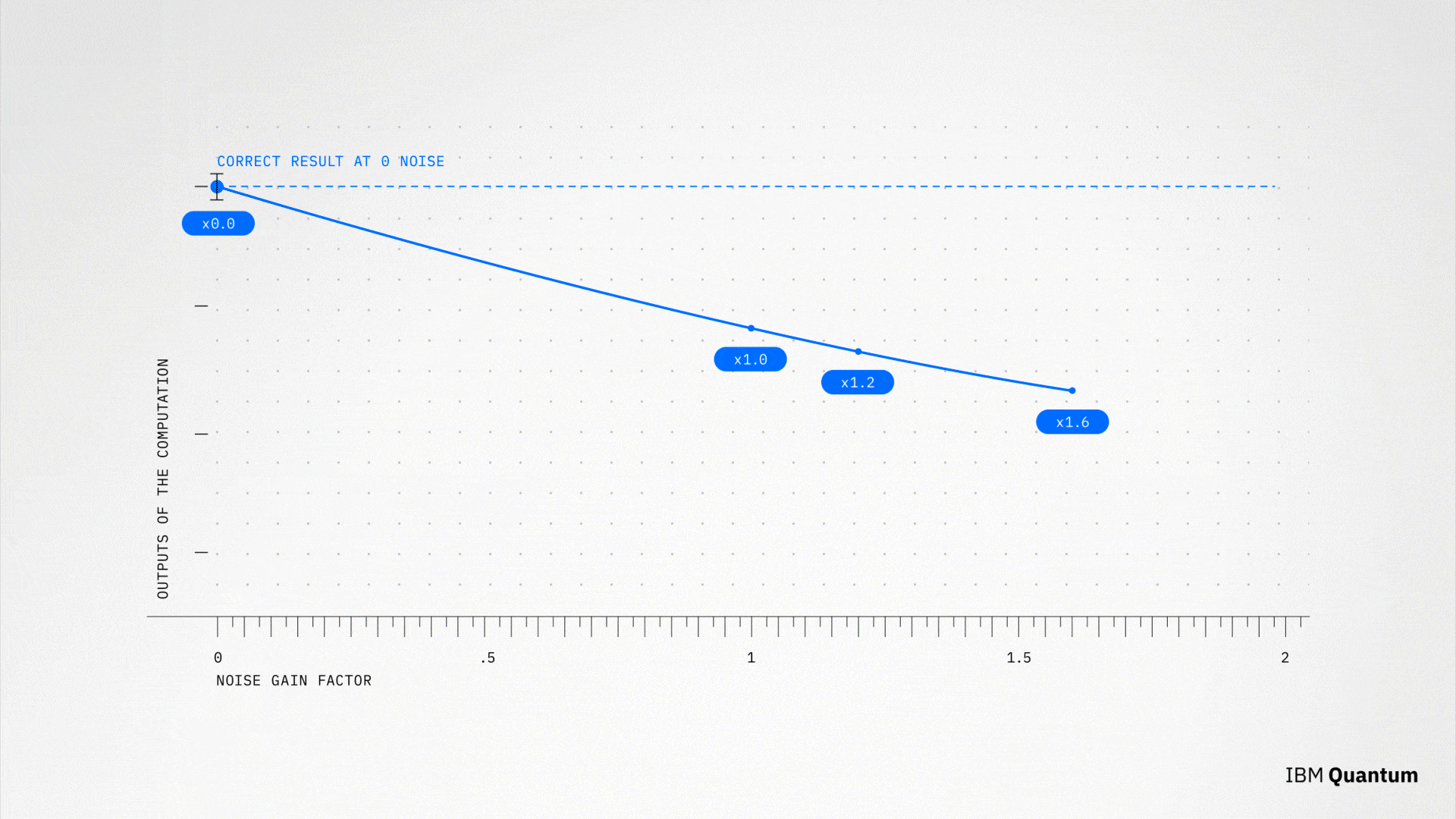
ZNEの例。 m=1、m=1.2、および m=1.6 に対するノイズ入りの結果を取得した後、m=0 すなわちゼロ・ノイズの時の値を外挿で求めることができます。
著者たちは、参照状態を使用することでZNEの結果を改善することができました。 |Ψsinglets⟩ に関連するエネルギーは正確に知られているため、彼らは正しい結果を得られるように回路のパラメーターを調整し、その後、既知の理想的なエネルギー値と、実験で得られてZNEによってエラー緩和されたエネルギー値の間の比率を計算しました。この係数は理想的な値と緩和された値のギャップを表すので、著者たちはこれを、パラメーター付きの量子回路から得られた他のエラー緩和結果を再調整するために使用しました。
結果
著者たちが行った実験で達成したことを以下ですべて再確認します。彼らは、XXZスピン鎖モデル および ハイゼンベルグ量子スピン鎖モデルの大規模バージョンに対する基底状態エネルギーの計算から始めました。彼らは変分プロセスに従うことで、これらの量子系をシミュレートするために使用する量子回路の最適パラメーターを見つけました。 変分プロセスでは、各回路の反復が古典的な行列積状態 (MPS) 方式を使用してシミュレートされます。
【注】変分プロセス
変分プロセスは、測定されたエネルギーの値を減らすパラメーター調整を繰り返す反復プロセスです。 変分プロセスの各ステップでエネルギーが測定され、エネルギーがもっと低くなる新しいパラメーターの値が計算されます。 そして特定の条件 (例えば、特定のレベルの正確さ) が満たされるまで、プロセスが繰り返されます。
このアプローチにより、著者たちは、量子コンピューターのノイズを考慮しないで、理想的な基底状態に対して最適なアンザッツの精度を評価することができました。結果として、特にゲート層の数を増やした時に、図に示すような良好な精度が得られました。
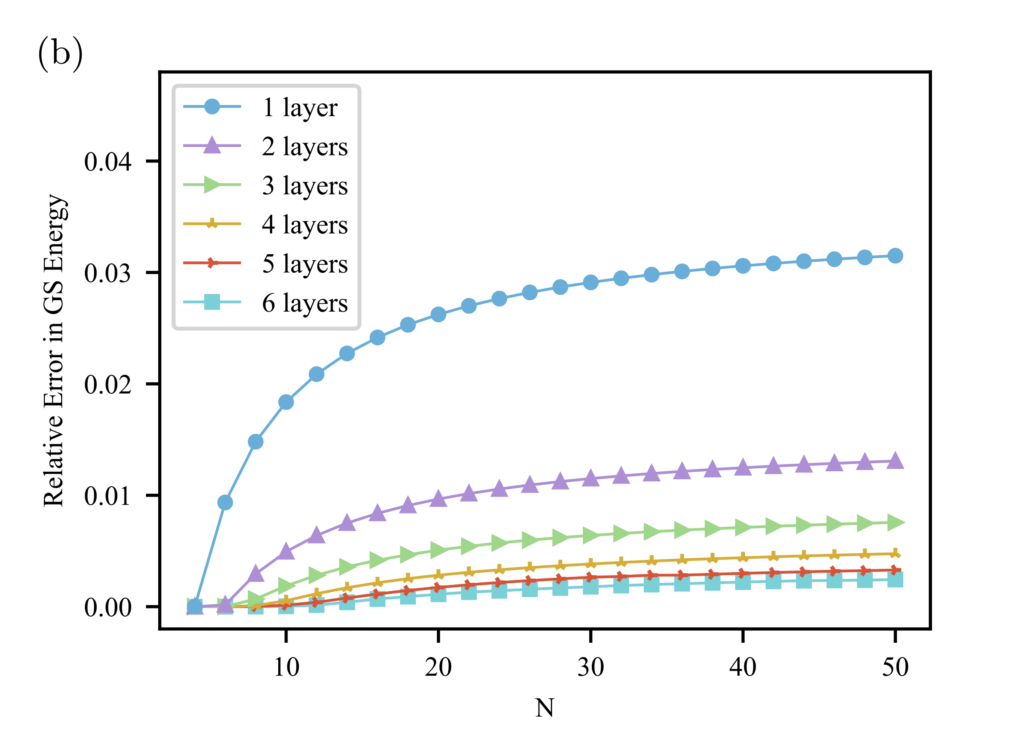
(論文の図3b) 最適パラメーターを持つ量子回路の古典的シミュレーションによって得られたエネルギーと、基底状態エネルギーとの相対誤差。 誤差は、量子ビット数 Nと、ゲート層数の関数として表示されています。
そこから、著者たちは、最適なパラメーターを使用して、実際のIBMの量子コンピューター上で量子回路を実装し、読み出しエラー緩和とZNEエラー緩和を使い、目的の結果を得ました。ZNEエラー緩和は、参照状態を使うことで改良されました。102量子ビットを使った計算で、XXZモデルの正確な基底状態エネルギーとの差異がわずか1.42%である結果を得ることができました。
著者たちのワークフローを理解する別の方法は、Qiskitパターンという、問題を量子コンピューターで解決する際の4ステップ・フレームワークで考えることです。
- 彼らは解こうとしている問題、すなわち量子モデルの基底状態エネルギーを求める問題を、対象問題の物理的性質に発想を得たアンザッツを含んだ、パラメーター付き量子回路を用いた変分プロセスに落とし込みました(map)。
- 彼らは 量子コンピューターの基本ゲートを使い、ベル測定を使うのに必要なショット数を最小化することで、この量子回路を目標量子ハードウェアに最適化しました(optimize)。
- 彼らは、量子ハードウェア上で量子回路を実行しました(execute)。
- 彼らは、彼らが提案している読み出しエラー緩和と、参照状態を使って改善したZNE手法を使って、結果を後処理しました(postprocess)。
著者たちは、実験中のこの変分プロセスを、MPSのような古典手法の助けを利用せずに、量子シミュレーション手法のみで実行することもまったく可能であるということを指摘しています。このことを彼らは、変分プロセスの初期に得られる回路と同等と考えることができる、ランダムなパラメーター値をもつ回路でも、計算できるエネルギー誤差が低いということによって主張しています。
もう1つの注目すべき結果は、ハイゼンベルグ・スピン鎖に関する著者らの研究から得られました。チームは、その手続きを XXZモデルについてのみだけ実装したのではなく、4から 102量子ビットまでのサイズのいくつかの系でハイゼンベルグ・スピン鎖を実装しました。それから著者らは、サイト当たりの近似的な基底状態エネルギー、すなわち粒子当たり平均基底状態エネルギーの推定値を導き出し、その値に基づいて無限長を持ったハイゼンベルグ・スピン鎖へと外挿しました。この理論的な、無限の長さのスピン鎖は「無限系の極限(Infinite system limit)」として知られています。ハイゼンベルクの場合には、著者たちは、外挿によって得られた値が Betheアンザッツによって得られた解から、4%しか異なっていないことを確認しました。Betheアンザッツは、ハイゼンベルグ・スピン鎖のような量子多体モデルを伴うシミュレーション問題に正確な解を求めることができる理論的な道具です。
【注】無限系の極限
無限系の極限は、粒子の濃度はおよそ一定のまま (量子系の)体積と粒子の数が無限サイズに近づく時に量子シミュレーションの問題に正確な解を計算することができるという点で有用なコンセプトです。
このような発見は、実用規模の量子ハードウェアが、確立された物理理論と良く一致した結果を提供できる能力を持っているということを示す、さらに強力な一つの証拠データと言えます。 全体として、Stony Brook大学チームのスピン鎖実験は、有用な量子系の特性を量子コンピューターで調査する上で、私たちにとって大きな前進をもたらしました。この将来の能力は、理論物理学と、材料科学などの実用的なアプリケーションの両方に、極めて大きな意味を持ちます。
Qiskit を使って参照状態を用いる ZNEを再現する
最後に、Python と Qiskit を使用して、Stony Brook大学の、参照状態を用いた ZNEの簡単な実装を見てみましょう。
簡単化のため、この例では、ZNE手法と参照状態の組み合わせを使って、ノイズを含んだ出力を緩和することができるような、パラメーター付き量子回路をトイ・モデルとして使っています。この回路は論文で実装されたものと同じではありませんが、この手法は一般性を持っていて、他のシミュレーションにも拡張することができます。
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
from qiskit_ibm_runtime import QiskitRuntimeService, Batch
from qiskit_ibm_runtime import EstimatorV2 as Estimator
from qiskit.quantum_info import SparsePauliOp
import numpy as np
from scipy.optimize import curve_fit
# Build the quantum circuit (“U” in the main text)
def build_ansatz(qc, parameters, N, num_layers):
for j in range(num_layers):
for i in range(N):
for i in range(N-1):
# Build the inverse of the quantum circuit (“U^-1” in the main text)
def build_reversed_ansatz(qc, parameters, N, num_layers):
for j in range(num_layers-1,-1,-1):
for i in range(N-2,-1,-1):
for i in range(N):
# Build the QuantumCircuit objects for different levels of noise (“m” in the main text)
def circuits_different_noise_levels(parameters, N, num_layers, repetitions, pm):
for rep in repetitions:
for iter in range(rep):
build_reversed_ansatz(qc, parameters, N, num_layers)
build_ansatz(qc, parameters, N, num_layers)
ansatz_isa = pm.run(qc)
circuits.append(ansatz_isa)
return circuits
# Exponential function for the zero noise extrapolation
def exponential_func(x, a, b, c):
# Exponential function re-scaled with the factor obtained with the reference state
def rescaled_exponential_func(x, a, b, c, r):
if __name__ == ‘__main__’:
# Getting the real quantum computer
backend = service.least_busy(operational=True, simulator=False)
target = backend.target
# Pass manager for transpilation
parameters_0 = np.zeros((N,num_layers)) # Parameters for our reference state (Identity circuit with all parameters equal to 0)
# Building the observable to measure and the quantum circuits
circuits = circuits_different_noise_levels(parameters_0, N, num_layers, repetitions, pm)
observable = SparsePauliOp.from_list([(s,1)]).apply_layout(layout=circuits[0].layout)
pubs = []
for i in circuits:
circuits = circuits_different_noise_levels(parameters, N, num_layers, repetitions, pm)
for i in circuits:
# Execute on quantum hardware
with Batch(backend=backend) as batch:
result = estimator.run(pubs=pubs,precision=0.01).result()
noisy_expvals = []
# Get the results
for samples in range(len(pubs)):
noisy_expvals.append(noisy)
noise_levels = [1, 3, 5] # noise level (“m” in the main text)
# Zero noise extrapolation for the Identity circuit (reference state) to get the rescale factor “r”
a_fit, b_fit, c_fit = params
zero_noise_limit_0 = exponential_func(0, a_fit, b_fit, c_fit)
r = (ideal_expval_0-c_fit)/a_fit
zero_noise_limit_0_correct = rescaled_exponential_func(0, a_fit, b_fit, c_fit, r)
# Zero noise extrapolation of our random circuit and zero noise extrapolation modified with the reference state factor “r”
# The accuracy of the expectation value obtained with the rescaled factor depends on the parameters obtained from the curve fitting process
a_fit, b_fit, c_fit = params
zero_noise_limit = exponential_func(0, a_fit, b_fit, c_fit)
zero_noise_limit_correct = rescaled_exponential_func(0, a_fit, b_fit, c_fit, r)
Stony Brook大学研究チームの開発した方法のような、巧妙にカスタマイズされた量子エラー緩和の実装は、実用規模の量子ハードウェアを使用して大規模で複雑な量子系を研究する上で重要です。
【注】Qiskit Runtimeでのエラー緩和
実用規模の実験は、Qiskit Runtime Estimatorに既に利用可能になっている量子エラー緩和手法を使って行うこともできます。ここには、計測エラー緩和、ZNE、そしてその他の手法がビルトインで提供されています。Qiskit Runtimeエラー緩和手法を使った実験については、こちらのチュートリアル をご参照ください。
過去10年間で私たちが目にしてきたような大きな技術進歩はありましたが、量子ハードウェアの出力は環境ノイズによって引き起こされるエラーの影響を依然として強く受けています。 研究対象の量子系をもっと正確に近似する結果を得るためには、量子エラー緩和やその他の後処理手法から可能な限り大きな効果を得る方法をまだ調査する必要があります。この探索は、量子コンピューターが計算をしながらエラーを訂正できるようになる、量子エラー訂正という将来の機能が利用可能になるまで続きます。
このブログで取り上げた論文は、モデルの既知の性質を活用することで、これらの手法の有効性を向上させる強力な例を示しています。それがここでは、読み出しエラー緩和のためにペアになった量子ビットの組み合わせのみを考慮するという方法、既知の参照状態を使用してZNEの結果を改善するという方法でした。
このような物理学的な根拠に基づいた洞察は、長年の理論研究の成果の上に構築されており、将来の量子シミュレーションにおいて重要な役割を果たす可能性があります。読者の皆様ご自身の研究にも価値を提供できる可能性がある、Stony Brook大学の実験で使用されたこれらの手法の詳細についてはぜひ著者たちの論文 をご参照ください。
この記事は英語版IBM Researchブログ「Advancing quantum algorithms for large-scale simulations of quantum spin chains」(2024年10月30日公開)を翻訳し一部更新したものです。

IBM Quantum, スタッフ・リサーチ・サイエンティスト
量子アルゴリズムや量子回路最適化など最適化分野を中心とした研究開発に携わる。

Qiskit SDK v1.3がリリースされました!
主な新機能や改善点、非推奨となった機能を含めて Qiskit SDK v1.3のリリースの技術的要点をご紹介します。 2024年12月4日に Qiskit SDK v1.3のリリースを発表しました! この最新リリースは、 […]
量子中心のスーパーコンピューターに必要なサーキット・カッティングを可能にするダイナミック・サーキット
Natureに掲載された新しい論文は、一つの量子プロセッサーでは実行不可能なサイズの量子回路を、二つの量子プロセッサーを接続して実行できることを世界で初めて示しました。 今日、世界で最も強力な古典的スーパーコンピューター […]
フォト・レポート:SEMICON Japan 2023 IBMブース
SEMICON Japan 2023に、IBMが出展しました。 本記事は、フォト・レポートとして、IBMブースで撮影した写真を掲載します。 IBMブースの外観 NorthPole(超省電力のエッジ向けデジタルAIチップ) […]

