量子コンピューティング

エラー訂正機能を持つ量子コンピューターでの演算

2024-05-13

カテゴリー IBM Research (コンピューティング) | 量子コンピューティング

記事をシェアする:

対称性と非ユークリッド幾何学からの視点

量子ユーティリティーの時代に入り、エラー訂正のような仕組みを持った大規模な量子コンピューターにおける、エラーのない計算の実行方法についての本格的な検討が進んでいます。エラー訂正を用いた場合、エラーから情報を保護するために追加量子ビットを使うので、エラー訂正を用いない場合よりも多数の量子ビットを使って量子情報を符号化します。

昨年、私たちはエラー訂正符号に量子情報を符号化する新しい方法を発表しましたが、この方法によって、以前に想定されていた¹よりも少ないオーバーヘッドでエラーのない量子コンピューターを構築することができるという見通しを持つことができました。qLDPC符号というコード体系に基づいているこのコードを私たちはグロス符号と呼んでいます。しかし、問題はまだあります。それは、情報を符号化した後に、どうやってそれに対して演算を行うかが未解決であるということです。

最近の研究²で、私たちのチームは、ラトガース大学の物理学者Shehryar SikanderとMITの数学者Elia Portnoyとの共同研究により、この問題の解決に向かって重要な前進を遂げました。その答えは、トポロジーと幾何学の領域にあります。私たちは、物理量子ビットのレイアウトとそこに保存する情報を幾何学的オブジェクトとして扱う形でqLDPC符号を研究し、隠されていた対称性を解き放つためにそれらのオブジェクトの数学的性質を探求しました。私たちは、この数学的探求から得られた知見が、私たちのグロス符号にも適用可能になることを期待しています。しかし私たちはまたこの旅を通じて、量子符号の形式になった量子ビットの挙動と物質そのものとの深い関係を発見しました。

qLDPC符号

最も基本的な説明として、エラー訂正は、エラー訂正を使わない場合よりも多くの物理的なハードウェアを情報表現に使うことで、エラーから情報を保護する冗長性を量子ビットに組み込む、と説明することができます。古典的なビットで最も素朴な例を考えてみるならば、1 ビットの情報を表現するために 3 つの物理ビットを使用するやり方です。そこでは、3ビットのうち2ビット以上が「0」に設定されていると「0」を、逆に2ビット以上が「1」に設定されている時は「1」を表現することができます。量子エラー訂正も同様の概念に基づいていますが、量子ビットに格納する追加的な情報を考慮するためにより複雑な構造を用います。

現在、量子エラー訂正符号では量子低密度パリティーチェック(qLDPC)符号とよばれる系列が最先端と考えられています。これらのアプローチの主な利点は、大規模化した時に、エラー訂正のために必要な追加量子ビットの数が従来の符号に比べて少ないということです。このオーバーヘッドは、情報を符号化する物理量子ビットの数 n と、情報を表現する論理量子ビットの数 k の比で測ることができます。上の例では、この比率は n 対 1 です。qLDPC符号ではこの率を定数に漸近させることができます。qLDPC符号が良いスケーリング特性を持つことを表すもう1つの重要な数値は、符号距離です。これは、いくつの量子ビットが壊れても、運びたい情報が破壊されないで済むかに関係します。上の例でこの距離は3です。距離の半分を超えるエラー数、この場合、2個かそれ以上のエラーが起きると論理的なビットの値が反転します。

では、新しいコードの課題は何でしょうか。

qLDPC符号は量子情報を効率的に符号化する方法ではありますが、符号化された情報に対して演算を実行する方法を見出す必要がまだあります。そしてそこには二重の課題があります。

まず、qLDPC符号では、論理情報がすべての物理量子ビット全体に分散しているため、どの物理量子ビットがどの量子情報を保持しているかを1対1の対応で説明することはできません。そのような符号化の仕組みのため、標準的な論理ゲートではすべての量子ビットを同時に対象とするしかなく、一部だけにアクセスすることはできません。
第二の問題は、qLDPC符号に対する論理ゲート操作が、論理Cliffordゲートに限られるということです。しかし、論理Cliffordゲートは古典コンピューターで効率的にシミュレートできることが理論的にわかっているため、それらを使うだけでは古典コンピューターに対する優位性が得られません。古典コンピューターに対する優位性がある汎用量子計算を実行するためには非Cliffordの論理ゲートもこのコード上で実装する必要があります。そのようなゲートを実行する方法は、マジックステート蒸留というプロトコルを通じた方法のみであり、それには空間的時間的に余分なリソースを消費することになります。

IBMの研究者と共同研究者による最近の研究²は、qLDPC符号とその基礎となっている対称性と幾何的形状について数学的理解を深めることで、両方の問題の解決に向けて重要な前進を遂げました。

超空間内のドーナツ

エラー訂正符号は、本質的には情報を量子ビットのレイアウト全体にいかに広げるかを決めるルールです。先の問題に挑戦するために、私たちは量子ビットのレイアウトを、量子ビットが存在する空間そのものを含めて、異なる視点で捉える必要がありました。

今日、従来的な符号、例えばよく知られた表面符号は、量子ビットを最も単純な幾何学的方法で扱います。つまり、2次元や3次元の空間を、三回右折すると出発点に戻るような正方形や立方体で視覚化するようなやり方です。このような幾何学をユークリッド幾何学と呼びます。しかし、空間を視覚化する方法はこれだけではありません。空間の形状やそれを記述する数学が異なっている非ユークリッド幾何学で考えることもできます。非ユークリッド幾何学は、私たち誰もが地球の球面上で経験しています。もし私たちが赤道から北極点に向かって出発したら、2回の右折で出発点に戻ることができます。また他にも風変わりな空間をいくつも考えることができます。例えば出発点に戻るのに5回の右折が必要だったり、あるいはもっと他の条件が必要だったりするような空間を想像することもできます。

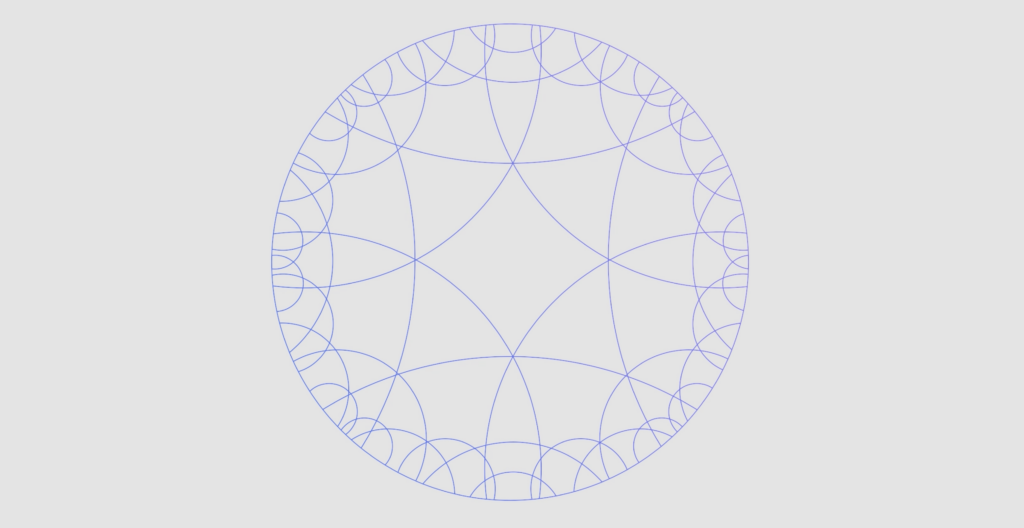
図1：M.C.エッシャーの絵画「Circle limit III」³。2次元双曲面のポアンカレ・ディスク・モデルにおけるタイリング（タイル張り）の芸術的な図示になっています。2次元双曲符号は適切な境界条件を持ったこのようなタイル上に定義することができますが、ここで量子ビットはこのタイルの辺（白い弧）の上に位置します。測地線は、ポアンカレ・ディスクの無限遠方の境界で始まり、そして終わる、同じ色を持った魚に沿った白い弧で表現されています。

qLDPC符号の非ユークリッド空間への埋め込みが、量子コンピューティングの時代に必要であると判明しました。

私たちの新しい研究では、双曲非ユークリッド3次元空間、つまり私たちが多様体と呼ぶものの上に量子ビットをタイルすることでqLDPC符号を構築しています。図1は、双曲空間とコードの、二次元における例示になっています。多様体は、ちょうど地球のように、局所的には平坦なユークリッド空間のように見えますが、全体的としてはそうではありません。しかし、地球よりももっと風変わりな、空間に「穴」を持っているような高次元の形状をした多様体を想像することもできます。

例えば、トーラス（タイヤ・チューブの形状）は、水平方向と垂直方向に特殊な境界条件を持つように湾曲している矩形領域に相当する二次元多様体です。これにはドーナツの穴とチューブ内部の空洞という2つの「穴」があります。高次元トーラスは、私たちが高次元空間には住んでいないため想像するのが困難ですが、三次元トーラスは次のように想像することができるかもしれません。すなわちそこでは、上下、左右、内外のいずれかの方向に向かって移動すると、元の場所に戻るように空間が歪んでいて、3つめの穴が存在しています。これは、図2(a)に示されています。

私たちの論文²では、このような風変わりな3次元空間の一種に量子ビットを敷き詰めてqLDPC符号を構築することで問題を解くことができることを発見しました。私たちのコードでは、大きな穴ほど良いコードになるという意味で、穴のサイズが符号距離を決定します。そして、穴の数は論理量子ビットの数を表していて、穴がたくさんあるほど多くの論理量子ビットを表現します。また、体積は物理量子ビットの数に比例します。したがって、最良のコードは、可能な限り多くの穴を持ち、そしてその穴が可能な限り大きくなるような多様体を台とするものです。

多様体と部分多様体

しかし、これではまだ元の質問に答えていません。どうやってqLDPC符号に非Cliffordゲートを実行すればよいでしょうか。そして、どうすれば同時にすべての量子ビットを操作するのではなく個々の論理量子ビットを操作できるでしょうか。それこそが、私たちが2次元多様体を超えた次元を必要とした理由です。カラー符号と呼ばれる、以前の研究は、高次元ユークリッド幾何学に基づくある種の符号を用いることで非Cliffordの論理ゲートが実装できることを示しています。今回、私たちは似たアイデアを3次元多様体に埋め込まれたqLDPC符号に適用しました。これによりqLDPC符号のスケーリングの利点に加えて、よりシンプルなカラー符号から応用した、論理ゲートを実行する能力が得られています。

まず、並列化可能なゲートを使用して一部の量子ビットを対象にすることです。私たちのコードでは、これは、球面上の円のように三次元空間の二次元サブセットに対する操作に相当しますが、私たちの場合、量子ビットを埋め込んだ、穴のたくさんある歪んだ理論的空間に適用されます。この空間をスライスする方法にはさまざまな方法があると想像することができます。アクセスできるゲートの数は、穴の数、すなわち論理量子ビットの数に従って指数関数的に増加します。

次は、非Cliffordゲートの実行です。ここでは、この高次元空間でのコード構築の際に生じた対称性に依存します。2次元の世界から3次元の世界に移行することで、新しい物理的性質にアクセスできるというイメージです。ここでは、位相欠陥、すなわち局所的な変形に対して変化しない、頑健な物理的オブジェクトが発生します。例えば流体中の渦やハードドライブの中の磁壁です。これらの位相欠陥を瞬間的に移動することで、非Cliffordゲートの実行が可能になります。

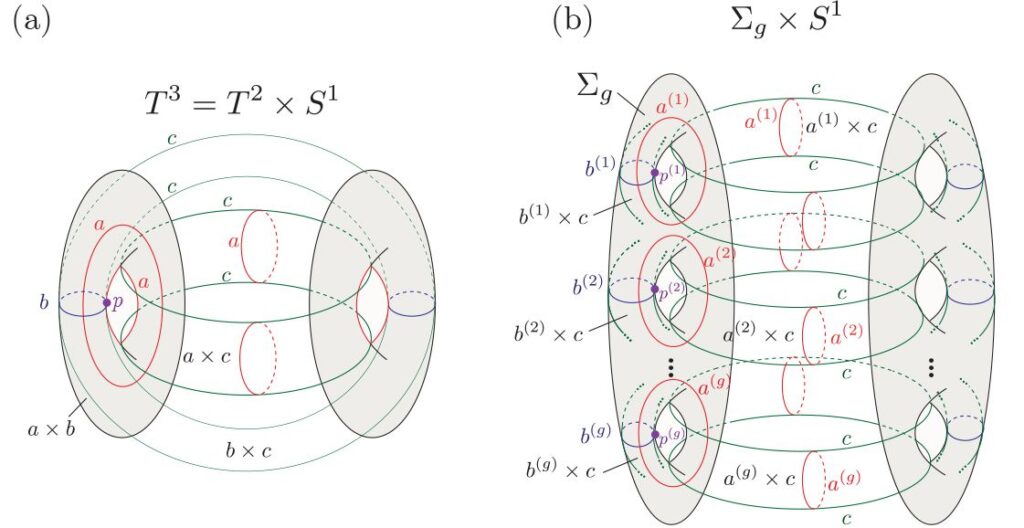
図2：私たちの論文²から (a)： 3次元トーラスは、2次元トーラスT²と円S¹の積として考えることができます。2次元トーラス上の非可縮ループ、つまり「穴」、にはaとbというラベルを付けていて、円に沿った別の「穴」にはcとラベルをつけています。ループa、b、cのポアンカレ双対非可縮膜は、他の2つのループの積、すなわちb × c、a × c、およびa × bによって形成される2次元トーラスです。それぞれのループとその双対膜は、単一点pで交差します。(b)：表面Σ_gと円S¹の積によって形成された3次元多様体上に定義された準双曲コード。表面上の非可縮ループにはa⁽ⁱ⁾とb⁽ⁱ⁾というラベルが付けられています。円に沿ったループにはcというラベルがつけられています。表面Σ_gを台とする非可縮膜がひとつあります。一方で、それ以外の膜はいずれも、2つのループの積として形成されたトーラスを台としており、a⁽ⁱ⁾ × c と b⁽ⁱ⁾ × cとしてラベルがつけられています。a⁽ⁱ⁾ × cとb⁽ⁱ⁾ × cとΣ_gが3つ組になったgセットの膜はg個の点 p⁽¹⁾, p⁽²⁾, … p^(g) で交わります。

興味深いことに、このような3次元多様体上の量子符号は、一種のトポロジカル量子場理論（TQFT）と等価であることがわかっています。量子場理論は、素粒子、光、そして私たちを取り囲み宇宙を満たす真空を含めて、微視的世界を最も正確に記述する理論です。また、さまざまな量子材料などその他の量子多体系を記述することができる強力な理論です。

私たちの目的においては、この理論は、多くの量子ビットで形成されている多体系として捉えることができる量子符号を説明してくれます。詳細は省略しますが、qLDPC符号上で非Cliffordゲートを実行することが、トポロジカル絶縁体といった有名な量子材料を支配するのと同じ物理学に基づいているということは、私たちのチームとメリーランド大学やカリフォルニア工科大学の共同研究者が前の研究⁴で指摘したことです。トポロジカル絶縁体は、内部が絶縁体で外部が導電体で、トポロジカルに保護されたエッジ電流を持っていて、物理研究分野として人気がある材料です。量子物質の物理学の利用が、量子コンピューティングの研究を導くことができるというのは非常に興味深いことです。

さて、これらのことはすべて、現実的には何を意味するのでしょうか。私たちは量子プロセッサーがハイパー・ドーナツのような形状を持って欲しいとは思っていません。その代わりに、短距離および長距離の接続回路を使用して、私たちはチップ上にエッチングされた量子ビットが、そのような高次元の形状を離散的に表現するように設計します。

コードの構築

私たちの論文²では、3次元多様体の3つの異なる系列を構築し、3つのqLDPC符号群を作成しました。これらはいずれもオーバーヘッドが一定、あるいはほぼ一定です。第一の構成では、種数g（「穴」の数が2g）を持った2次元双曲面と、gに対して対数的にスケールする円の積を用います。g=1の場合（3次元トーラス）は図3(a)に図示されており、一般のgの場合は図3(b)に図示されています。オーバーヘッド（物理ストレージとそれが符号化する論理情報の比率）は、物理量子ビットの総数に対して対数的にスケールします。符号距離も、物理量子ビットの総数に対して対数的にスケールします。

第二と第三の構成では、その積にさらに工夫を加え、円の長さを定数に設定します。この違いにより、第二の構成はほぼ一定のオーバーヘッドを、第三の構成は一定のオーバーヘッドを持つようになります。第二の構成は対数の平方根の距離を持ちますが、第三の構成の符号距離は現在のところ不明です。

この研究の残りの部分は、3次元多様体をより深く研究するための数学の開発に焦点を当てています。この分野はそれまでの数学で十分に探求されていませんでした。この研究はまた、量子状態の複雑さと基礎となる多様体の幾何学的性質やトポロジーの深い関係を確立しました。

大きなブレイクスルーを果たしたこの研究は、一定、あるいはほぼ一定のオーバーヘッドを持つ量子LDPC符号における非Clifford論理ゲートの初めての研究です。この発見は、qLDPC符号の論理ゲートと、3次元多様体のトポロジーと幾何学的形状、そして、対応するトポロジカル量子場理論における高次対称性の間の深い関係に基づいています。この研究で得られた洞察は、本論文で研究されているqLDPC符号の系列に限らず、より一般的な鎖複体に基づいている、qLDPC符号一般における論理ゲート構造の理解に光を照らすことになります。そういったコードには量子エキスパンダー符号やグロス符号が含まれます。

この研究は、アメリカエネルギー省、科学局、国立量子情報科学研究センター、量子アドバンテージ・コデザイン・センター（C2QA）から、契約番号DE-SC0012704で資金援助を受けています。

参考文献：

S. Bravyi, A.W. Cross, J.M. Gambetta, D. Maslov, P. Rall, T.J. Yoder. High-threshold and low-overhead fault-tolerant quantum memory. arXiv:2308.07915 (2023). https://arxiv.org/abs/2308.07915| ↩
G. Zhu, S. Sikander, E. Portnoy, A.W. Cross, B.J. Brown. Non-Clifford and parallelizable fault-tolerant logical gates on constant and almost-constant rate homological quantum LDPC codes via higher symmetries. arXiv:2310.16982. https://arxiv.org/abs/2310.16982| ↩
Dunham, D.: Transformation of hyperbolic Escher patterns. Visual Math. 1, (1999). https://www.d.umn.edu/~ddunham/isis4/index.html| ↩
M. Barkeshli, Y.A. Chen, S.J. Huang, R. Kobayashi, N. Tantivasadakarn, G. Zhu. Codimension-2 defects and higher symmetries in (3+ 1) D topological phases. SciPost Physics 14 (4), 065 (2023). https://scipost.org/SciPostPhys.14.4.065| ↩