Mthree Qiskit拡張による測定エラー緩和

記事をシェアする:

Mthreeは、Qiskitのエコシステムから提供されている強力なツールで、測定エラーへの対処において他の多くの方法よりも速く正確です。

量子コンピューターは、古典コンピューターでは実現できないスケールで、重要な問題を解決することができる潜在的な力を持っていますが、環境にあるノイズによって起こされるエラーの影響を受けてしまいます。量子計算で実用的な問題に取り組むためには、エラーを補正する手法を利用しなければなりません。研究者たちは、最終的には、量子コンピューターの演算中にエラーが生じるのと同時にその訂正も進められるような未来の機能である、量子エラー訂正を実現することを期待しています。しかし、そのエラー訂正が実用的になるまでは、量子エラー緩和のような、よりシンプルなエラー対処方法に頼ることになります。

量子エラー緩和とは、演算が一通り終わってからノイズの影響を差し引くことを可能にする後処理のテクニックです。エラー訂正が現実になるまでの間の直近の量子実験では、エラー緩和の活躍が期待されます。2023年に発表したIBM量子コンピューターの「ユーティリティー」実験では実際にエラー緩和が重要な役割を果たしましたし、量子エラー訂正や将来の真に大規模な量子アプリケーションにおいても、必要なオーバーヘッドを削減するためにエラー緩和は重要であると考えられる十分な根拠があります。

しかし、量子エラー緩和の可能性を最大限に引き出すためには、最新のエラー緩和手法を実験に適用する際に役立つツールを、私たちは継続的に開発し続けなければなりません。より具体的には、研究を加速するのに役立つ、よくテストされ、パフォーマンスの高いソフトウェアを提供しなければなりません。これらのツールを使って実験することにより、量子計算科学者はエラー緩和の効果的な利用のための重要な洞察を得られるものと思われます。

今回のこのブログでは、qiskit-extensionモジュールで現在利用可能なQiskit-Extensions/mthreeという1つのツールについて詳しく紹介します。簡単にMthreeまたはM3と呼ばれているこのソフトウェアパッケージは、マトリクス・フリー測定緩和（M3）手法を実装していて、量子計算プラットフォームでスケーラブルな測定エラー緩和を実現するように設計されています。

測定エラーとは

M3は、「測定エラー」に特にフォーカスした量子エラー緩和パッケージです。現在または近い将来の量子コンピューターでは様々な種類のエラーが存在しますが、測定エラーはその中でも最も一般的なものです。回路中の量子ビットから情報を取り出すために行う測定は、量子コンピューターに対するすべての命令の中で最大のエラー率を持っています。したがって測定エラーは、今後しばらくの間使用することになる深さの浅い回路では特に多大な影響があります。幸いなことに、測定エラーの効果は次のように単純な線形システムとしてうまく記述されます。

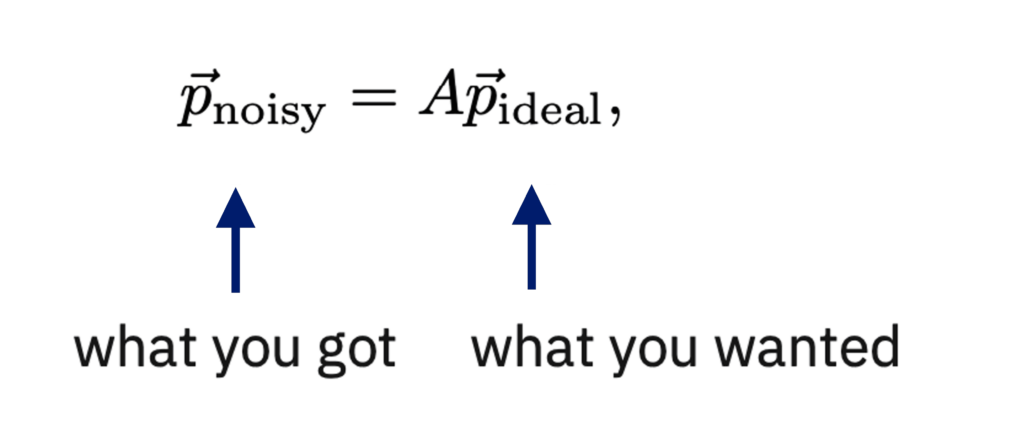
ここで、は測定ノイズがある場合に測定されたビット列の出力確率ベクトルであり、は測定ノイズを伴わない場合の出力確率ベクトルです。そして、Aは、与えられた理想的な測定出力を、実際に測定したノイズ入り出力に確率的にマップする、サイズ の「アサインメント」行列（nは量子ビットの数）です。

ナイーブな言い方をすれば、計測されたビット列の出力確率ベクトルにアサインメント行列の逆行列 を乗じることで計測エラーを緩和することができます。そして、個の基底状態について回路を実行し、計算基底に対してそれらを測定することでAを構成することができます。しかし、量子ビット数が多い時は、nに対してAとの次元数と、走らせなければならない回路の数が指数関数的に増加するため、このアプローチは現実的ではありません。

このリソース要件を軽減する1つのアイディアは、複数の量子ビットのエラーに相関はないと仮定して、各量子ビットについてのサイズ のアサインメント行列のテンソル積を計算することでAを近似することです。この際に、個々の量子ビットについて基底状態 0と1に対する回路ペアを用意し測定するので、合計で  個の基底状態回路を必要とします。テンソル積近似を使うことで、キャリブレーション回路の必要数を、計測される量子ビットの数と線形になるように削減することができますが、アサインメント行列の次元数は という指数関数的大きさのままです。これが大部分の測定エラー緩和手法が直面する主な問題の一つです。

M3はどのようにして量子測定エラーに対処するか

この問題への対処に有用なのがM3です。もし測定エラーがたとえば1%程度ぐらいの小さい値で、回路が十分にサンプリングされていれば、ノイズ混じりの出力ビット列は理想的なビット列をすべてサブセットとして実際に含んでいる、という事実をM3は利用します。信号はノイズに隠されているのです。

のA行列を利用する代わりに、ノイズあり出力における k個の異なるビット列によって定義される、サイズに削減された部分空間においてエラー緩和を行うことができます。kは最大でも、たかだか収集されたサンプル数（つまりショット数）に等しいということで、特にnが大きい時に kはよりもずっと小さい値で済ませられます。

この考え方をより詳細に理解するために、シンプルな2量子ビットの例を考えてみます。

4つの可能なビット列のうち3つのビット列、0（00）、2（10）、3（11）が得られ、それらの確率は下図に示すようにで表されるとします。十分なショット数と、エラー率が数%程度であるとすれば、図に示す黄色の領域にある項は無視できます。このときA行列の次元は から に削減されます。この削減の影響は、量子ビット数が大きい時にはとても大きいものになり、Aの行列サイズを劇的に削減します。

もちろん、出力ビット列の数がとても大きいので、削減されたアサイメント行列 が利用可能なメモリーよりもまだ大きいという場合もあります。このような場合、M3は行列を計算することなく、線形方程式を反復的に解きます。

反復的な解法は一般には遅くなります。しかしM3は、計測エラーが十分小さいので は対角成分が支配的であるという事実を利用します。前処理のテクニックと を初期値にして反復を開始することで、桁違いに少ないメモリーを使用しつつ、わずかな反復回数で収束を得ることができます。

以下に示すのは、M3と他の緩和手法を精度と速度の面で比較したグラフです。ここでは、IBMの量子コンピューター Brooklynシステム上で動作するGHZ回路を用い、量子ビット数を42まで変えて性能を測定しました。

42量子ビットで、M3は最大でも1.2秒以内にエラーを緩和し、約1メガバイトのメモリーを使います。これは、この場合、疎行列A全体を保存するのに必要なメモリーサイズが約580PiBであることを考慮すれば素晴らしい値です。580PiBは、世界最速のスーパーコンピューターの一つとしてよく知られている富岳のメモリーの120倍です。

しかし、大規模な回路で測定エラーの影響を効率的に緩和できるといっても、コストがないわけではありません。M3を適用すると結果の精度は向上しますが、不確実性も増加させます。

この不確実性は、より多くのサンプリングを行うことで補償できます。サンプリング・オーバーヘッドの量は、Mという乗数的因子によって上限が求められますが、Mは、削減されたアサインメント行列の逆行列の1ノルム、すなわち として見積もることができます。これは、不可避的な精度劣化を補うためにM3が必要とする追加ショット数を表します。

M3の利用

M3を支える手法の理論的な理解はこの辺までとして、どうやってこれを実際に使うかを示すシンプルな実例で締めくくりましょう。以下のコードを実行するためには、このページに載せましたコマンドを実行してM3をインストールする必要があります。

以下のコードは、Bernstein-Vazirani（BV）アルゴリズム回路を構成し、FakeSherbrookeと呼ぶ架空のシステムで実行します。ここには合計で8つの回路があり、回路ごとの量子ビットの数は2から1つずつ増やします。全てのBV回路は、1がm個連なるm量子ビット列を作るように設計されています。たとえば、3量子ビットの回路は実行すると111を生成します。

 

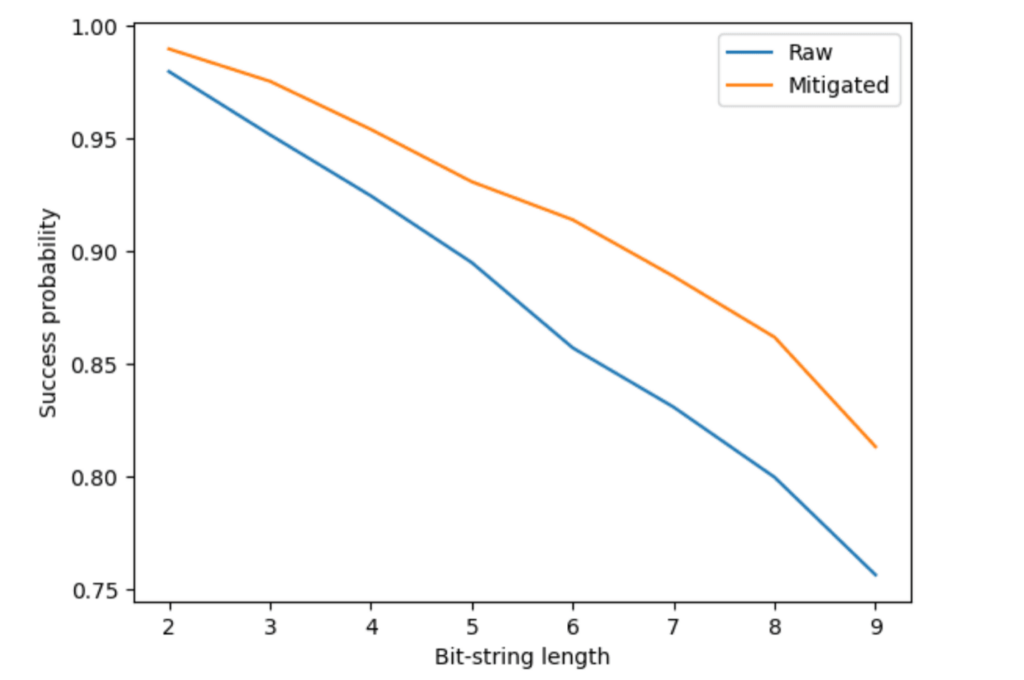
FakeSherbrookeバックエンドから得られる結果は、測定ノイズを含めて何種類かのノイズの影響を受けています。ノイズの効果は、下図で”Raw”とラベルされた成功確率のグラフに見られるように、回路のサイズが大きくなるほど大きくなります。

私たちは、ノイズありの結果に対するM3を次に示す3ステップで実装します。まず、仮想量子ビットをマップする物理量子ビットを特定します。次に、測定ノイズのプロファイルを取得するために物理量子ビットに対してキャリブレーションを行います。そして最後に、回路実行で得られたカウントに対して補正を行います。元の結果に対する成功確率の改善は、同じ下図で ”Mitigated”とラベルされたグラフに見ることができます。

M3をさらに改善する

Bernstein-Vaziraniアルゴリズムは、回路途中での測定を利用することで、さらに大幅に効率的に実現することができます。そして回路途中での測定をM3測定エラー緩和と併用すれば、ここに示されたように、成功確率を大きく改善することができます。

もちろん、どんなコードにも改良すべき点はあります。現在、私たちの研究における主要な課題のひとつは、ボトルネックを取り除く方法を見つけることです。現在、M3における主要なボトルネックは を構成する規格化ステップです。

これは、単純な浮動小数点演算を必要とする、とても並列度の高いタスクです。多数の並列スレッドの利用が劇的なスピードアップをもたらす、GPU（Graphics Processing Units）の理想的なユースケースです。

私たちは、量子コミュニティーの他のメンバーにこのM3が有用であると理解してもらいたいと願っており、どなたでもこのオープンソース・プロジェクトへの貢献に歓迎しています。ぜひ、量子エラー緩和手法の限界を押し上げ、量子計算の真のユーティリティー、そしていずれは量子優位性を実現へと向けて協業させていただきたいと私たちは望んでいます。

 

---

この記事は英語版IBM Researchブログ「Exploring measurement error mitigation with the Mthree Qiskit extension」（2024年4月3日公開）を翻訳し一部更新したものです。