【リレー連載】わたしの推しノード –隠れた関係を見つける名探偵「ベイズノード」が変数間の因果構造を解き明かす

記事をシェアする:

 

日本アイ・ビー・エムの小林竜己です。

2016年の入社以来、前職までのIT業界や製造業の仕事で得た様々なスキルや知識を活かし、データサイエンティストとして、自動車関係のお客様を中心に、日々、お客様のデータ分析やAI開発のお手伝いをしています。最近はAI人材教育に携わることも多く、IBM Cognitive Technology Academyの講師を担当する一方、お客様のニーズに応じた様々なカスタマイズ研修もご提供しています。仕事の中ではPythonを使う場面が多くなってきていますが、プログラミングが不要で直感的操作により高度な分析モデルを構築できるSPSS Modelerは一定の人気があり、私もこれまで多くの場面で使ってきました。今回は、個人的な思入れから、SPSS Modelerのメジャーな機械学習のモデリングノードに押されがちで使われることが少ないと思われるベイズノードについて、使い方とその価値をご紹介します。  

 

ベイジアンネットワークとは

ベイジアンネットワーク（Bayesian Network）は、事象間の因果関係をグラフで表現する数理モデリングの手法です。ベイジアンネットワークという名称は、この手法の研究者で、2011年のACMチューリング賞（計算機科学分野のノーベル賞といわれる）の受賞者でもあるJudea Pearlにより1985年に命名されました。

ベイジアンネットワークは、変数をノードとみなし、ノードを結合してグラフ構造を作ります。ノードの結合には向きがあり、これにより、因果関係の影響関係が表現されます。大事な約束として、結合されたグラフ構造は巡回しない、つまり、ノードの結合を辿って元ノードには戻らない有向非循環グラフが前提となります。ノードは確率変数と呼ばれ、ノード間の因果関係を確率変数の関係で表現します。

ところで、ネットワークと呼ばれはしますが、ニューラルネットワークとは全く別のものなので注意が必要です。ネットワーク構造の観点では、ベイジアンネットワークのノードは全てユーザが与えた変数ですが、一方、ニューラルネットワークは、ユーザが与える変数は入力層と出力層のみで、その間には隠れ層が設けられ、より複雑な構造を持ちます。学習方式の観点でも、ベイジアンネットワークとニューラルネットワークは全く異なります。詳しくは書籍などでご確認ください。

 

TANとMarkov Blanketのグラフ構造

さて、ベイジアンネットワークは、因果関係を表現可能な有向非循環グラフ一般を指しますが、SPSS Modelerのベイズノードでは、TAN（Tree Augmented Naïve Bayes）とMarkov Blanketというとてもシンプルな、制限のあるグラフ構造が用意されています。   SPSS Modelerにはありませんが、Naïve Bayesという最も単純なベイジアンネットワークがあります。以下の表では、Naïve Bayes、TAN、Markov Blanketそれぞれについて、グラフ構造の特徴と使用上のメリットについてまとめました。

 

 

それぞれのベイジアンネットワークのイメージ図は以下の通りです。Yは目的変数、Xは説明変数を表しています。それぞれ特徴的なグラフ構造をしていることが分かりますね。  

 

 

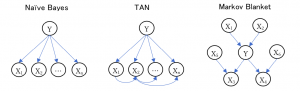
分析データの変数の間に因果関係が存在するような場合、ベイズノードを用いることで、こういったグラフ構造を提示してくれます。因果関係のような明確な関係性がないデータでも、他の機械学習アルゴリズムが教えてくれない変数間の隠れた関係性が浮かび上がり、分析対象をより深く理解するきっかけを与えてくれます。

 

 Irisデータセットをベイズモデルに投入する

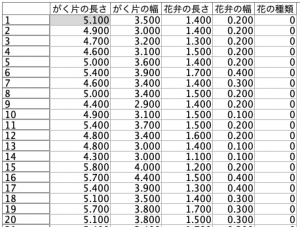
では、ベイズモデルの概要をご説明しましたので、次はベイズノードの使い方を見てみましょう。分類問題を構成できるデータであれば大丈夫ですので、機械学習でお馴染みのIrisデータセットを使うことにします。データは全体で150レコードあり、説明変数はがく片と花弁のそれぞれの長さと幅の4つ、目的変数はあやめ（Iris）の花の種類とで構成されています。以下の通りです。

• 目的変数：花の種類（0：セトナ、1：バーシクル、2：バージニカの3値）
• 説明変数：がく片の長さ、がく片の幅、花弁の長さ、花弁の幅の４変数

実際のデータは以下のテーブルの通りです。 

 

 

ストリームは、ベイズノードのTANとMarkov Blanket、それから比較のためにC5.0（決定木）ノードでモデルナゲットを作ることにしました。以下のようにとてもシンプルな構成です。

 

 

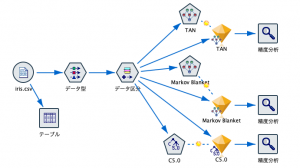
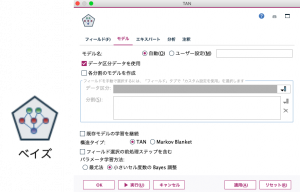
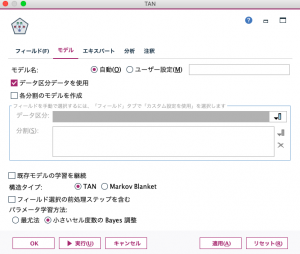
次に、ベイズノードの説明に移ります。ノードの画面には、フィールド、モデル、エキスパート、分析、注釈の5つのタブがあります。フィールド、分析、注釈の３つのタブは、他の機械学習アルゴリズムのノードと同じですので、以下では、モデルとエキスパートのタブ画面を対象に、TANとMarkov Blanketのモデル学習について説明します。   最初に、TANのモデルを学習します。設定する項目はシンプルで、以下の通りです。

• 構造タイプ：TAN
• パラメータ学習方法：小さい度数のBayes調整
• エキスパートタブ：変更せず
• 分析タブ：「予測変数の重要度を計算」にチェックを入れる

   

 

パラメータ学習方法には、２つの選択項目があります。SPSS Modelerのマニュアルには以下のように書かれています。今回、Irisデータセットはとても小さいので、「小さいセルの度数のBayes調整」を選ぶことにしました。

• 最尤法 : 大きなデータセットを使用する場合は、このボックスを選択します。これがデフォルトの設定です。
• 小さいセルの度数のBayes調整 : 小さいデータセットの場合、ゼロ度数の上限の可能性とともにモデルがオーバーフィットする危険性があります。このオプションを選択すると、ゼロ度数の効果および信頼できない推定効果を減らす平滑法を適用してこれらの問題を緩和します。

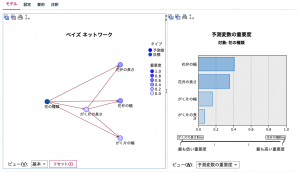
以上を設定した後、実行ボタンを押下してモデル学習を行うと、以下の画面を持つモデルナゲットが得られました。左半分に描かれているのがTANによるグラフ構造で、右画面が予測変数（説明変数のことです）の重要度です。

 

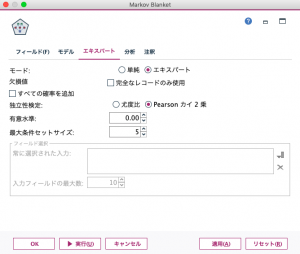
  では次に、以下の条件で、Markov Blanketのモデル学習してみます。モデルタブの設定は、上で行ったTANの設定とよく似ていますが、今回はエキスパートタブの設定をしてみましょう。  

• 構造タイプ：Markov Blanket
• パラメータ学習方法：小さい度数のBayes調整（データセットが小さいため）
• エキスパートタブ：「エキスパート」にチェックを入れ、「Pearsonカイ二乗検定」を選び、独立性の検定の有意水準を01から0.00に変更する。
• 分析タブ：「予測変数の重要度を計算」にチェックを入れる

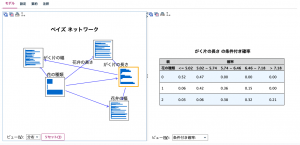
  以下がエキスパートタブの画面です。上記の内容が設定されていることが分かります。ちなみに、フィールド選択という設定がグレーアウトされていますが、有効化するには、モデルタブの「フィールド選択の前処理選択を含む」にチェックを入れます。フィールド選択は、大規模な説明変数が存在する場合、あらかじめモデル学習の候補にする変数を選択して登録するために使います。

 

 

ちなみに、Markov Blanketで、独立性の検定の有意水準をデフォルトの0.01から0.00に変更した理由は、カットオフされてしまって学習結果のグラフ構造から排除されてしまう説明変数を表示するためです。有意水準を0.00に設定することで、Markov Blanketらしいグラフ構造を得ることができます。しかしながら、モデルの精度を追求する場合は有意水準をデフォルト以上にするのがよいでしょう。   さて、実行ボタンを押下すると、以下のMarkov Blanketのモデルナゲットが得られました。TANのグラフ構造と比較すると、まったく異なりますね。特に、「がく片の長さ」、「がく片の幅」の２つは、目的変数である「花の種類」の子ノードである「花弁の長さ」、「花弁の幅」の親ノードになっており、目的変数とは直接の関係を持たないことが明らかとなりました。これは驚きです。 TANでは目的変数とすべての説明変数がエッジ（接続の線）を持つ必要があったのですが、Markov Blanketではその必要がなく、より自由に変数の関係性を調べた結果、このような構造が推定されたわけです。おそらく、あやめの花の種類は花弁の形状に強く依存するのでしょう。そして、がく片の形状は、花の種類よりも、花弁の形状に強く関係性があるということがデータから推測されたわけです。

 

 

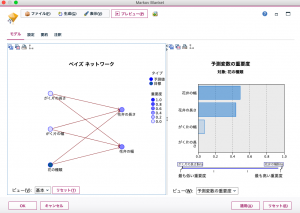
このように、ベイズノードを用いると、手軽に、変数間の関係性をグラフ構造で表現できます。そして、手元にあるデータに内在する変数間の関係性や因果関係を解きほぐしながら、より確かにモデリング対象を表現できるモデル（グラフ構造）を探すことができます。このように、明示的に変数の関係性を考えるプロセスがモデル構築と一体化していることがベイズノードの特徴です。他の機械学習アルゴリズムを使った場合に類似の作業があるとすれば、変数間の独立性の検定や相関分析を行うといった変数選択がそれにあたるでしょう。しかしながら、ベイズノードは、変数の関係性を「向き」を含めて捉えようとし、因果関係まで一気に踏み込んでいく点はとても大胆です。私が長年、ベイジアンネットワークに魅かれる理由はまさにそこにあります。なんて大胆かつ魅力的でしょう！  

 

グラフ構造の条件付き確率を観察する

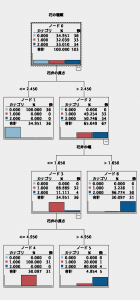
もう少しだけ、ベイズノードのモデルナゲットの読み解き方を見てみましょう。   モデルナゲットのモデルタブの左下のビューを「分布」に切り替えると、左半面のグラフ構造の表示が変わり、丸印のノードが、横方向棒グラフに切り替わります。一つの棒グラフをクリックすると、右半面の表示が、「予測変数の重要度」から「条件付き確率」の表に切り替わります。ベイジアンネットワークは、確率変数で構成されるグラフ構造であると説明しましたが、まさに「条件付き確率」の表は、ノードの関係をノード同士の値の組合せ単位での条件付き確率を保持しています。条件付き確率表は、専門用語でCPT（Conditional Probability Table）と呼ばれます。   以下の画面は、TANで学習したモデルについて、左半面のグラフ構造の「がく片の長さ」をマウス選択し、左半面に「がく片の長さの条件付き確率」の表を表示した例です。実際のグラフ構造では、親ノードである「花の種類」ノードから「がく片の長さ」ノードに接続していますが、表はそれに対応しています。表の行方向が「花の種類」、列方向が「がく片の長さ」です。なお、名義尺度である「花の種類」は0、1、2の3値が3列に対応していますが、「がく片の長さ」の連続変数のため、自動的に値域が分割されて、個別の値域毎に列が作られていることに注意しましょう。表の各セルは個別の条件付き確率です。例えば、「花の種類」が0で「がく片の長さ」が5.02未満の時、条件付き確率は0.52であることが分かります。

 

 

ベイズノードと決定木ノードとの比較

そういえば、今回、C5.0（決定木）ノードでもIrisデータセットを学習をしていました。C5.0のモデルタブでは次のように設定しました。１本のツリーを生成するだけです。

• 出力形式：ディシジョンツリー
• 出力形式のチェックボックス：チェックせず
• モード：シンプル
• モードの優先：精度
• モードの予想されるノイズ：0

  結果を見ると、正答率は、TANもMarkov BlanketもC5.0もそれほど違いはありませんでした。なお、Markov Blanketは、モデル精度を高めるため、独立性の検定の有意水準を0.01に戻して実施しました。

• 学習データの正答率
  • TAN 94.17%、Markov Blanket 91.26%、C5.0 98.87%
• テストデータの正答率
  • TAN 97.87%、Markov Blanket 97.87%、C5.0 97.87%

 

C5.0が出力した決定木は以下の通りでした。  決定木は、見て分かる通り、分類問題を解くためのデータの読み解き方（ルール）を表現したものになっています。当然ながら、ベイジアンネットワークが推定する変数の依存関係や因果関係を表現したものではありません。決定木とベイジアンネットワークは知識表現がまったく異なるといえます。

決定木は、実用的な問題解決のための知識表現であり、一方、ベイジアンネットワークは、愚直に、変数間の関係性を見出そうとします。しかしながら、どちらのアルゴリズムも、モデルの中に、人が読んで使える、確かな知識を作り出そうとしているところに共通点があります。かつて、機械学習のことを「データマイニング」と呼んでいた時代がありましたが、決定木とベイジアンネットワークは方向は違えど、データから知識をマイニングするというその時代の空気を持った老舗の機械学習アルゴリズムといえるでしょう。

 

おわりに

近年の機械学習アルゴリズムは、とにかく当たればよいではないですが、分類や回帰の予測性能を高度に追い求めてきた結果、モデル化対象をよりよく理解し、理解した結果を人に伝えることを犠牲にしてきてしまった面があると思います。サポートベクターマシーン、ニューラルネットワーク、ディープラーニング、さらにはアンサンブル学習（複数作成するモデルの予測結果を総合して判断する）といった手法自体も、とにかく予測の精度を求める方向での発展だったといえます。私はこれ自体を否定するものでは決してありません。

近年の「説明可能AI」研究の高まりを見るにつけ、予測精度の追求の中で置き去りにされてきた「モデルの解釈・説明性」への再検討が始まったように感じており、そんな中、分析対象の変数の因果関係をモデル化しようと試みるベイジアンネットワークの方向性は、人に伝えることを前提にした「モデルの解釈・説明性」の一つのアプローチを示しているように思えてなりません。

ベイジアンネットワークは、モデル精度の点で他の機械学習アルゴリズムに負けてしまうことが多く、主役の場に躍り出ることはほぼありませんが、物事を深く考える学者タイプ（名探偵！）のノードとして、使い方によってはとても価値のある働きをするノードであると述べて、筆を擱きたいと思います。

次回のリレー連載、推しノード#19は日本情報通信株式会社の近澤様がCPLEXの最適化ノードについて解説されます。

 

 

→SPSS Modelerの詳細についてはこちら

→わたしの推しノード（リレー連載）バックナンバーはこちら   

→これまでのSPSS Modelerブログ連載のバックナンバーはこちら

→SPSS Modelerノードリファレンス（機能解説）はこちら

→SPSS Modeler 逆引きストリーム集（データ加工）はこちら

 

 

 

小林　竜己

日本アイ・ビー・エム株式会社
グローバル・ビジネス・サービス