SPSS Modeler ヒモトク
Modelerデータ加工Tips#20-ワイブル分布を当てはめて故障を予測する
2021年10月18日
カテゴリー Data Science and AI | SPSS Modeler ヒモトク | アナリティクス | データサイエンス
記事をシェアする:
みなさんこんにちは、日本IBMの都竹(つづく)高広です。
日本IBM子会社のISEでNetworkエンジニアとして11年過ごした後、データサイエンティストとして8年間さまざまな業種のお客様企業のデータ分析やシステム構築に取り組んで来ました。2021年6月から親会社に出向し、現在はIBM Client Engineeringという新しいセールス組織でIBM Garage手法を用いた提案活動にデータサイエンティストとして関わっています。
このブログは毎回楽しみにしています。特に出題される詰め将棋が面白くて、回答を事務局に送ったら何度か取り上げていただけたのは大変光栄です。SPSS Modelerユーザー歴は、2012年に社内でアンケート分析をして以来9年になります。
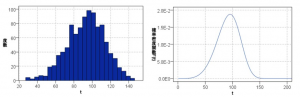
Deep Learningが華々しい機械学習全盛期の昨今ですが、今回はあえて古典的な統計学手法であるワイブル分布の推定を取り上げてみます。ワイブル分布は、正規分布のようにデータ傾向を表す分布の一種で、その生い立ちからも故障傾向や製品寿命を調べる時に使われます。私自身も、いろいろな寿命的傾向を捉える方法として使ってきました。しかし他にも様々な用途があり、例えば風車を設計するときの風速の分布としても使われているようです[1]。
分布にはパラメータがあります。例えば正規分布は平均値と標準偏差の2つのパラメータで表現されますが、ワイブル分布は形状mと尺度η(イータ)の2つのパラメータで表現されます。ワイブル係数とも呼ばれる形状パラメータmが特に優秀(私の勝手なイメージ)で、この値によっていろんな形に変えることができる=様々なデータに適用しやすいというのが特徴です。
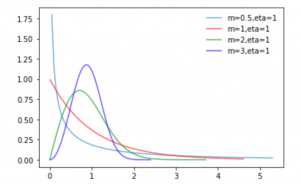
m < 1では、初期故障が多い分布
m = 1では、時間に対して一定の故障率となる分布(偶発的故障)
m > 1では、時間経過とともに故障率が大きくなる分布(摩耗的故障)
と言われています。m=3あたりは正規分布にかなり近いですね。
そして分布の推定とは、観測で得られたデータ(1件1件はばらついた寿命を持つ)をヒストグラム化して、そのヒストグラムにフィットするワイブル分布の曲線を探すという作業です。これは例えば、全国統一模試の得点をヒストグラム化して正規分布を当てはめる(平均値μと標準偏差σを求める)ことと同じです。その結果、自分が成績上位何%に属しているのかが分かるわけですね。ワイブル分布でいうと、あと何年でどれくらいの故障が発生するのかが分かることになります。
ところで、ワイブル分布はかなりStatisticsな手法なので、データマイニングツールであるModelerでは出来ないと誤解されている方がいらっしゃるのですが、いえいえ、ちゃんと出来ます。ワイブル以外の分布の推定にも応用できますので、データの傾向を分布という形で捉えたい時に使える技だと思います。
最も簡単にできる方法として、推しノードでも登場したシミュレーションノードを使います。さて前回出題した例題を見てみましょう。
例題1:「正規分布のデータを生成する」
以下のヒストグラムのような正規分布するデータ100,000件をご自分で作ってみてください。利用するノードはシミュレーションノードがお勧めです。
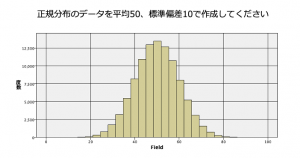
これは入力ノードの一種であるシミュレーション生成ノードの基本的な使い方の練習でした。シミュレーション生成ノードを置いて、シミュレーションしたフィールドを1行追加し、分布は「正規」、パラメータは平均を50、標準偏差を10に設定します。生成する件数の設定は拡張オプションの「ケースの最大数」ですが、デフォルトで100,000件です。
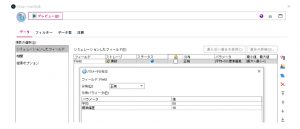
そしてヒストグラムノードを繋いで、フィールド名Filedのヒストグラムを書くと完成です。
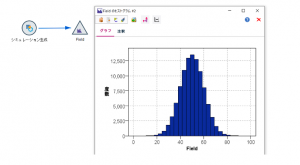
(ちなみに私はグラフ表示のデフォルトを上図のように「文字を12pt」「背景なし」に変更しています。特に文字を大きくしておくと報告資料に貼る時に見やすくなってオススメです)
例題2:「ワイブル分布の確率密度関数のフィールドを生成する」
次はヒストグラムの元データではなく、分布を表す関数(確率密度関数)です。与えられた200件のデータ(横軸t)に対し、ワイブル分布の関数のフィールド(縦軸F(t))を生成して、以下のようなグラフを作ってください。
ワイブル分布の関数の式やパラメータの値は以下の通りです。手数は問いません。
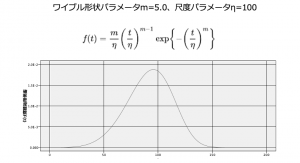
例題データ
利用するデータは、以下です。
https://raw.githubusercontent.com/yoichiro0903n/blue/main/weibull_input.csv
(リンクを右クリックして「リンク先を保存」またはブラウザで開いてからページを保存します)
この問題は、数式をCLEM式で表現する練習でした。この数式を見た瞬間に目をそらしたくなりますが、よく見てみてください。割と簡単な分数やべき乗などで構成されています。1つずつ組み立てて行けば、CLEM式で表現できます。
フィールド作成ノードでmとetaを数字で定義した後、確率密度関数F(t)というフィールド名で問題の数式をCLEM式で表現します。CLEM式はこんな感じです。こう見ると頑張れば書けそうですよね。
(m/eta) * (t/eta)**(m-1) * exp(-1*(t/eta)**m)
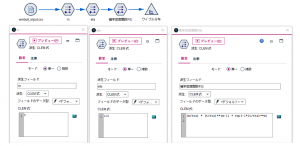
さて、本題に入ります。例題1のように、シミュレーション生成ノードを使うと様々な分布に従うデータを作成できます。まず今回の本題で使う架空の故障記録のデータ1000件を作ってみましょう。
シミュレーション生成ノードを置き、1フィールド追加して、分布は「ワイブル」、パラメータは形状パラメータmを5、尺度パラメータηを100にします。パラメータの設定名は製品マニュアル上に見つけられなかったのですが、形状1がη、形状2がmのようです。スケールは原点の位置をずらすためのオプションパラメータなので今回は0に設定します。
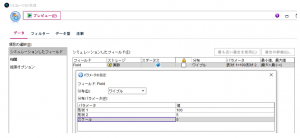
件数をデフォルトの100,000件から減らして、1000件にします。拡張オプションの「ケースの最大数」で設定します。
生成された入力データ1000件をヒストグラムで確認するとこうなります。なお、フィールド名はフィルターノードでtに変更しています。
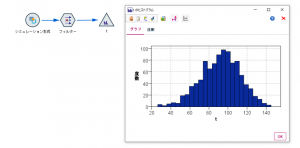
1000件なので少しギザギザが目立つ形となっています(よりリアルに近い感じ)。なお、シミュレーション生成ノードのランダムシードを変えると形が若干変わります。ここまでが準備です。
今、この1000件の車の部品の寿命(時間t)という観測データが得られたとします。この部品の寿命をワイブル分布に当てはめて、時間tと故障率の関係を明らかにしてみます。
最も簡単な方法は、推しノード#21で三井住友海上火災の木田さんが紹介されたシミュレーションの当てはめノードを使う方法です。この入力データの先に、出力タブにあるシミュレーションの当てはめノードを接続し、そのまま実行すると新たなシミュレーション生成ノード(ノード名:Sim Gen)が自動生成されます。この生成されたノードが、データに最も適合する分布とそのパラメータを表現しています。
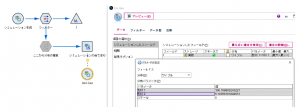
推定結果として得られたワイブル分布のパラメータは、m=5.103…、η=101.109…です。もしここでワイブル以外の分布が選択されていた場合は、「適合の詳細」ボタンからワイブル分布を手動で切り替えができます。
これでワイブル分布の推定が完了です。得られた分布から車の部品が故障する確率、具体的には経過時間tに対する故障発生の比率を求めることができます。ストリームでは、パーセンタイルを求めてその時刻tを表にしてみます。
Sim Genノードにデータ分割ノードを接続し、フィールドtに対して分位フィールドを作ります。パーセンタイルだと1%区切りで細かすぎるので、今回は20分位(5%区切り)を使っています。
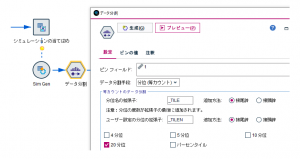
作成されたフィールドt_TILE20は1〜20の分位を表す数値ですが、パーセンタイルに読み替えられるように5倍しています。文字列化しているのは後ほどグラフを書く時に区分毎に色分けしたいためです(数値型だと色がグラデーションになるので)。
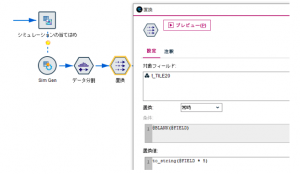
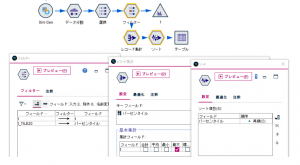
フィルターノードでフィールド名を変更した後、各パーセンタイル値を表にするためレコード集計ノードとソートノードを以下のように設定します。パーセンタイル(20分位)毎に最大のtを算出してパーセンタイル値とみなしています。
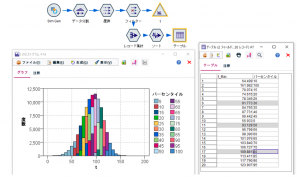
これで、パーセンタイルで色をつけたtのヒストグラムと、各パーセンタイルの値の表が出来ました。tの単位が1ヶ月だった場合、82ヶ月(6.8年)で30%が故障し、93ヶ月(7.8年)で50%が故障し、110ヶ月(9.2年)で80%が故障することが分かります。
さて、ここでもう1つのワイブル分布推定の方法をお見せします。シミュレーションの当てはめノードを使わずに、データ加工系のノードのみを使って愚直に計算する方法です。実を言うと私、この便利なシミュレーションノードの存在を長らく知らず、2年前まで以下の方法で強引にワイブル分布の計算をやっていました。もっと早く知っていれば。。。
やや複雑な計算を含むので、説明は簡潔にして最後にサンプルストリームを添付します。
ワイブル分布の推定は、ワイブルプロット[2]という手法を用います。時間Tと累積故障率Q(T)を以下の式でxとyに変換して散布図をプロットし、そのプロットに最もフィットする直線y=ax+bを求めます。形状パラメータmと尺度パラメータηは、得られたaとbから計算できます。
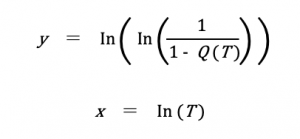
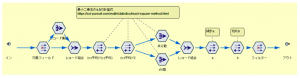
計算式もさほど複雑ではないですし、推定する作業は線形モデルノードを使えば簡単に求められます。ストリームの全体像はこんな感じです。
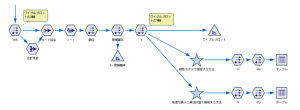
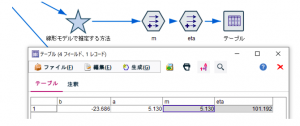
新規フィールド作成ノードで随時計算結果を加えていきます。最初はワイブル分布のX軸であるln(t)ですが、時間Tの自然対数を取るだけなのでCLEM式は log(t) です。Y軸は少しややこしくて、log(log(1/(1-‘累積確率’))) というCLEM式になります。累積確率はレコードをtの昇順にソートして全体の何番目かという比率で表します(省略)。これでワイブルプロットを散布図ノードで書いてみるとこうなります。
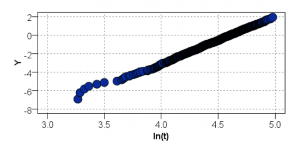
この横軸を説明変数、縦軸を目的変数として線形モデルノードで回帰モデルy=ax+bを作ると、a=5.130、b=-21.686となります。(ストリームでは「線形モデルで推定する方法」スーパーノード内です)
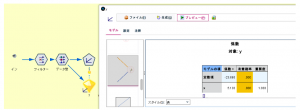
さてこの方法の問題点は、欲しい値aとbがモデルナゲットノードの中に入っていることです。この2つの値を手書きで写すのは非効率です。1つの方法として、モデルナゲットをPMMLファイルとして書き出し、そのファイルをXML入力ノードで読み取るやり方があります。線形ノードから生成したPMMLファイルは、XML形式でこの2つの係数を含んでいます。PMMLファイルのエクスポート方法は、ファイル > PMMLのエクスポートです。
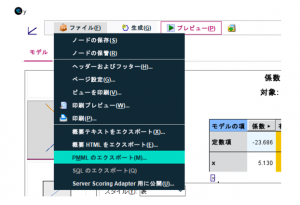
エクスポートしたPMMLファイルをXML入力ノードで読み込み、aとbをデータ化します。2つ入力ノードを置いているのは係数の値と係数名を別々に取得しているためです。
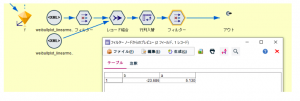
さて、aとbが得られたので、mとηを求めます。mはaの値をそのまま使えます。ηはCLEM式で書くと exp(-1*(b/a)) です。これでワイブル分布の推定結果であるmとηが得られました。完成。
このPMMLファイルに一度書き出す方式は、手作業が入るためちょっと厄介です。ここをPMMLに頼らずにデータ加工系のノードだけで計算的にy=ax+bを求めるストリームも作ってありますので、興味ある方は見てみてください(「地道な最小二乗法計算で推定する方法」スーパーノード内です)。
使用したストリームは、以下からダウンロード可能です。
https://github.com/yoichiro0903n/blue/blob/main/weibull_stream.str?raw=true
今回はSPSS Modelerでのワイブル分布推定のやり方にフォーカスしてかなり理想的なデータを使いましたが、現実世界の問題ではこんなにきれいなヒストグラムにはなりません。データの収集方法の問題や、得られたデータに偏りがあるなど、様々な課題に対処していく必要があります。サンプル数が少ないケースでは推定結果もずれやすくなります。ワイブル分布を実践的に使う様々な研究がなされていますので[3]、実務で使う場合はそれらの先行研究や事例を踏まえた方がより良い結果に結びつくでしょう。
Modeler詰将棋!次回のTipsから出題
次の2つの例題にチャレンジしてみてください。Modeler TipsのIBM運営者によれば賞品は一切ないものの、正解すると名誉と自信がもれなくついてくるそうです。
例題1:「併買パターンを集計する」
すでに顧客毎にカテゴリ購買有無を示すテーブルができている前提で、カテゴリの併買を集計してください。

例題データ
利用するデータはこちらです。
https://raw.githubusercontent.com/yoichiro0903n/blue/main/sampledatacross2.csv
(リンクを右クリックして「リンク先を保存」またはブラウザで開いてからページを保存します)
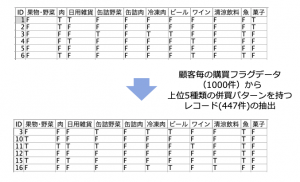
例題2:「併買パターン上位5つのどれかに該当したレコードを抽出する」
例題1の結果、冷凍肉と缶詰野菜を併買するパターンが最多で、173件でした(例題1の表を参照)。同じように同時に購入されるパターン上位5位を見つけ、そのどれかに該当するレコードを抽出しなさい。
ぜひチャレンジしてみてください。
さて次回のTips# 21はアクセンチュアの赤石さんが執筆されます。SPSS ModelerとPythonの比較で例題を解説!なのだそうで私自身も楽しみです。

都竹 高広
日本アイ・ビー・エム株式会社
テクノロジー事業本部 クライアント・エンジニアリング本部
データサイエンティスト
[1] https://www.jstage.jst.go.jp/article/jweasympo1979/28/0/28_0_369/_article/-char/ja/
[2] https://weibull.com/hotwire/issue8/relbasics8.htm
[3] https://www.i-juse.co.jp/statistics/xdata/reliability-shimizu-slide.pdf
データ分析者達の教訓 #22- 予測モデルはビジネスの文脈で語られ初めてインパクトを持つ
Data Science and AI, SPSS Modeler ヒモトク, アナリティクス...
皆さんこんにちは。IBMの坂本です。 SPSSを含むデータサイエンス製品の技術を担当しています。 このリレー連載ブログはSPSS Modelerの実際のユーザーで第一線で活躍するデータ分析者に、データ活用を ...続きを読む
Women in Data Science Tokyo @ IBM 2024 開催レポート
Data Science and AI, IBM Data and AI
こんにちは。IBM西戸です。 今年で5回目のWomen in Data Science (WiDS) Tokyo @ IBM が2024年6月14日に初の会場とオンラインのハイブリッド開催されました。会場は2024年2月 ...続きを読む
法務・AIリスクのスペシャリスト三保友賀が語る「ダイバーシティー」 | インサイド・PwDA+7(後編)
Data Science and AI, IBM Sustainability Software
日本IBMにて法務、特にAI倫理・リスクのスペシャリストとして、そして同時にLGBTQ+コミュニティー*1やPwDAコミュニティー*2のアライとして積極的に活動している三保友賀さんにお話を伺いました。 前編での法務・AI ...続きを読む


