Modelerデータ加工Tips#05-@OFFSETで車両の時刻と座標から速度や距離を得る

記事をシェアする:

みなさんこんにちは。株式会社JALエンジニアリングの竹村 玄と申します。
弊社はJALグループの航空機材全般の点検・整備を行う整備会社で、2016年よりSPSS Modelerを使って故障予測分析に取り組んでいます。故障予測分析というのは数年にわたって蓄積している「航空機からフライト中に取得される各種センサーデータ」と「整備履歴データ」を統合的に分析することで、現在運航している航空機に対して近い将来に発生する不具合の発生を予測し、それに対して予防的な整備処置を実施することで不具合発生を未然に防止するというものです。航空機のセンサーデータは機種にもよりますが数千パラメータほどの種類のデータがあり、なかには１Hz以上のサンプリングレートで取得されているものもあり、そのセンサーの時系列変化(１データ前からの変位量)に着目したい場合などは今回ご紹介する@OFFSETが大変有用で、このノードは私たちが故障予測分析をしていく上でのマストアイテムになっています。

 

Nレコード上の値を参照する@OFFSET

@OFFSETの説明から始めます。IoTデータを扱う方は例えば１分前との温度差を求めたり（@DIFF）、マーケティングデータでも７日間移動平均(@MEAN)を作りますよね。これまでも三菱自動車の伴さんは推しノード#07で、ビデオリサーチ の田村さんもTips#03にて紹介されてきました。@関数はModelerユーザーの最も強力な武器のひとつですし、他ならぬ航空機のセンサーデータから予知保全に取り組む私どもはこれがないと仕事になりません。

まずは基本的な利用イメージだけ説明します。@関数はフィールド（列）への働きかけをする関数で、例えば@OFFSET(列名,N)でN行上を参照せよを意味します。

 

 ２点間の距離を測る方法

 

本編を解説する前提として先に触れておきます。２つの座標（緯度と経度）間の距離を測る方法です。航空機のように長距離移動を想定する場合、地球の表面が球体である点を考慮した計算方法を用いますが今回は特定都市部のタクシー移動ですので少し簡略化します。

直角三角形の斜辺と捉えて三平方の定理を用いるのですが、地球が完全な球体ではなく楕円である点を考慮したヒュベニの式を使うことにします。

 

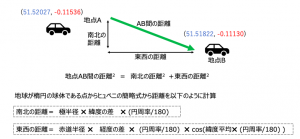
前回のTips#04の出題時の式を再掲します。円周率pi やコサインはModelerの関数から呼び出せますが、赤道半径と極半径を間違えずに入力する必要があります。一度作成したらスーパーノードなどでルーチン化しておくと便利そうです。

 

例題１  「車両の時刻と座標から平均速度を求める」

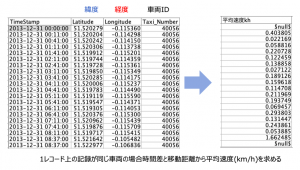
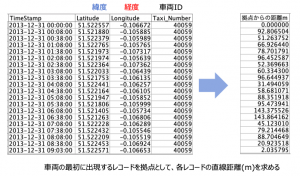
元データと完成イメージはこちらです。

 

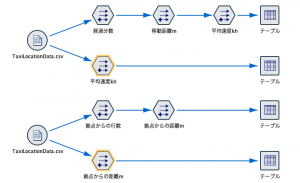
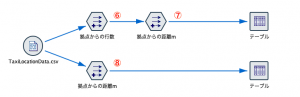
わかりやすい３手詰め（②③④）と、それをまとめた１手詰め（⑤）の２通りの完成ストリームです。

 

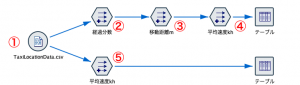
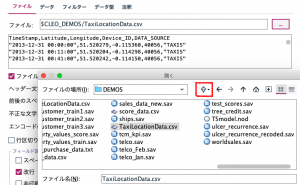
①で読み込むデータはSPSS Modelerをインストールすると同梱されるサンプルデータTaxiLocationData.csvです。DEMOSというフォルダを確認ください。赤枠のダイヤモンドのアイコンから「Demos」を選択するとその直下にあるはずです。

 

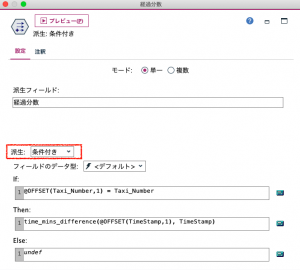
最初のフィールド作成ノード②では、派生モードを「条件付き」とします。続けて電卓ボタンをクリック、式ビルダを起動して以下のように設定します。「If」の項目にはタクシーI Dの１レコード上と現在のタクシーI Dが一致したら、を表すために「@OFFSET(Taxi_Number,1) = Taxi_Number」と記述します。

「Then」には２つのタイムスタンプの時間差を分で表す「time_mins_difference(開始、終了)」を用います。開始時刻は1レコード上の「@OFFSET(TimeStamp,1)」を終了時刻は該当時刻である「TimeStamp」です。

「Else」には、タクシーI Dが切り替わったらヌル値にするため「undef」と記述します。

 

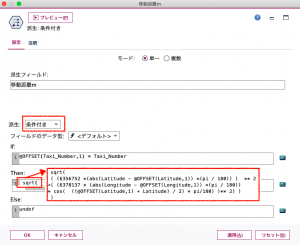
③のフィールド作成も②と同様に派生モードは「条件付き」として、「If」と「Else」にも同じ設定を行います。「Then」はすでに紹介したヒュベニの公式を利用して記述します。

sqrt( ( (6356752 *(abs(Latitude – @OFFSET(Latitude,1)) *(pi / 180)) )  ** 2　+( (6378137 * (abs(Longitude – @OFFSET(Longitude,1)) *(pi / 180)) * cos(  ((@OFFSET(Latitude,1) + Latitude) / 2) * pi/180) )** 2) ))

 

 

最後に④を設定して完了です。メートルや分を調整しながら距離を時間で割り算して速度を求めます。

 

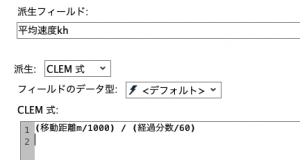
④までをひとつのノードで統合したものが⑤です。式は次の通り。

( sqrt(  ( (6356752 *(abs(Latitude – @OFFSET(Latitude,1)) *(pi / 180)) )  ** 2　+　( (6378137 * (abs(Longitude – @OFFSET(Longitude,1)) *(pi / 180)) * cos(((@OFFSET(Latitude,1) + Latitude) / 2) * pi/180) )** 2) )) /1000) / (time_mins_difference(@OFFSET(TimeStamp,1), TimeStamp)/60)

 

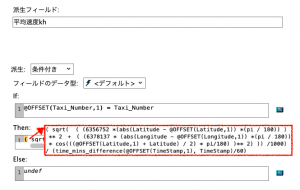
出題時にも触れているのですが、それぞれの車両はあり得ない瞬間移動をしている場合や、運転手が、ほぼサボっているように心配になりますが、ダミーデータとのことです。

 

例題２  「出発点から各レコード時点の直線距離を求める」

先の例題では直前のレコードとの比較でしたが今度は、タクシーI Dが最初に記録された座標をそのタクシーの拠点と仮定し、以降のレコードと拠点間の距離を直線で求めてみます。

 

このケースは@OFFSETを応用してカウントアップを使う２手詰めと、１手詰めで説明します。

 

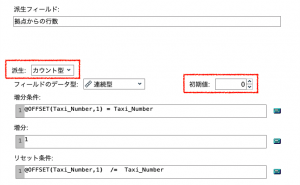
まず⑥のフィールド作成で、タクシーI D毎に通し番号を作成します。派生モードを「カウント」、初期値ゼロにします。カウントアップ条件を、例題１と同じ「@OFFSET(Taxi_Number,1) = Taxi_Number」として、リセット条件を「@OFFSET(Taxi_Number,1) /= Taxi_Number」にします。1レコード上と同じタクシーならひとつずつカウントアップし、別のタクシーに切り替わるとカウントがリセットされます。

 

出来上がりのテーブルは以下のとおり。４レコード目でタクシーが別I Dになるのでカウントがリセットされています。

 

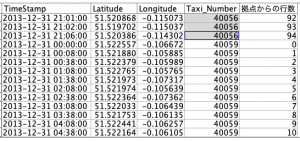
これができると@OFFSET(Taxi_Number,拠点からの行数)を使って初期レコードと当該レコードの比較が可能になります。

あとは⑦で、例題１でも利用した距離の式にそのまま当てはめればOKです。

 

sqrt( ( (6356752 *(abs(Latitude – @OFFSET(Latitude,拠点からの行数)) *(pi / 180)) )  ** 2)　+( (6378137 * (abs(Longitude – @OFFSET(Longitude,拠点からの行数)) *(pi / 180)) * cos(((@OFFSET(Latitude,拠点からの行数) + Latitude)/2) * pi/180) )** 2) )

 

出来上がると以下のようになるはずです。

 

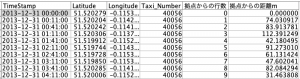
⑥⑦で実行した内容をほぼ、ひとつにまとめることができます。

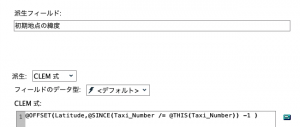
フィールド作成ノード⑧では以下のようにCLEM式を記述します。

sqrt( ( (6356752 *(abs(Latitude – @OFFSET(Latitude,@SINCE(Taxi_Number /= @THIS(Taxi_Number)) -1)) *(pi / 180)) )  ** 2)　+ ( (6378137 * (abs(Longitude – @OFFSET(Longitude,@SINCE(Taxi_Number /= @THIS(Taxi_Number)) -1)) *(pi / 180)) * cos(((@OFFSET(Latitude,@SINCE(Taxi_Number /= @THIS(Taxi_Number)) -1)+Latitude) / 2) * pi/180) )** 2) )

 

⑥のカウントと近い方法を「@OFFSET(Latitude,@SINCE(Taxi_Number /= @THIS(Taxi_Number)) -1 )」で表現しています。@SINCEと@THISの組み合わせを利用して該当する条件が何レコード上で成立しているかを値で返します。この場合、タクシーI Dが切り替わってから何レコードかを得た上で、そのレコードの緯度を求めています。

この方法はレコードに最初に登場するタクシーだけ計算対象外になる弱点があるため、ダミーレコードを用意するか、関数をさらに工夫する必要があります。

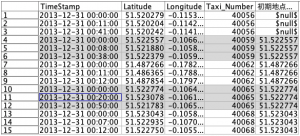
文章では伝わらない場合、元データに以下のフィールド作成をしていただけると、よく理解いただけると思います。

 

最初の５つのタクシーI Dの冒頭３レコードを表示しています。ID40056は、一番最初のタクシーI Dなので、この式が残念ながら有効ではないのです。

 

実はModelerにはShapeやPolygonなどの地理空間を扱う空間処理関数が準備されていて、そちらを用いて距離を求める方法もあり、どなたかがこのTipsで触れてくださることを期待しています。

 

Modeler詰将棋！次回のTipsから出題

 

次の２つの例題にチャレンジしてみてください。Modeler TipsのIBM運営者によれば賞品は一切ないものの、正解すると名誉と自信がもれなくついてくるそうです。

 

例題１：「カテゴリ別商品ランキングを作成する」

取引データから以下の商品ランキング表を作ってみてください。利用ノードは６つです（６手詰め）。結果のフィールド名はどのようなものでも結構です。

 

例題２：「客単価向上に貢献した商品のランキングを作成する」

顧客の売上実績を軸に商品のパフォーマンスについて調べます。優良顧客はどの商品を購入するのでしょうか。フィールド名は気にせず、５手詰めです。

 

例題データ

 

東京図書様に許可をいただき「実践IBM SPSS Modeler　 ～顧客価値を引き上げるアナリティクス」の紹介ページにあるダウンロードサンプルデータ「sampletranDEPT2015.csv」を利用いただけます。

→データのダウンロードはこちらから

 

いかがでしょうか。IBM所属のSPSS Modeler 凄腕棋士は例題１に５分、例題２には９分要したとのこと。

次回のTips# 06はファミマデジタルワンの橋本さんに例題の解説をいただきます。

ご期待ください！

 

→SPSS Modelerの詳細についてはこちら

→Modelerデータ加工Tips バックナンバーはこちら

 

 

 

竹村　玄

株式会社JALエンジニアリング

技術部技術企画室