身近な疑問をヒモトク#01-幹事の悩み！オンライン飲み会の部屋割りは最適化で解決

記事をシェアする:

 

皆様こんにちは！IBMの中島と阪本です。データサイエンス系のソリューションを担当しています。

２０２２年の新シリーズ「身近な疑問をヒモトク」が始まりました！このシリーズでは、日常の疑問をデータサイエンスの観点を取り入れて解決していきます。並行してSPSS Modelerのイチオシ機能を掘り下げて紹介する「ブログで学ぶSPSS Modeler」も連載開始していますのでご覧ください。

 

さてシリーズ第１回では、「大人数でのオンライン飲み会のベストな部屋割り」をテーマに考えてみます。

この時期、部署の大規模な新年会をオンラインで開催するという人も多いのではないでしょうか。その際、会話しやすさを考えメンバーを少人数グループの部屋（ブレイクアウトルーム）に割り振っていることも多いはず。しかし部屋割りが意外と厄介です。「どういうメンバーを同じ部屋にすると会話が弾むだろうか」、「リモートで部署の雰囲気に慣れない新入社員はアドバイザー社員とペアにした方がいいかな」、「各グループの若手社員とシニア社員の割合を半々くらいに調整してほしいという依頼があった」など考慮することが意外と多かったりして幹事の悩みは尽きません。実際にこの記事はある同僚が、オンライン飲み会で性別や年代、職種がなるべくばらつき且つ１次会から３次会までで違う人と話せるようなオンライン部屋割りに難儀して相談してきたことがきっかけになってます。

そんな時に役立つのが数理最適化です！最近特に関心が高まっていることもあり、機械学習やデータ分析などのキーワードと合わせて「数理最適化」あるいは単に「最適化」という言葉を耳にする機会も多いのではないでしょうか？今回は「オンライン飲み会の部屋割り」を題材に数理最適化について紹介します。

 

数理最適化で何ができるか？

ところで、数理最適化について皆さんどのくらいご存知でしょうか？「飲み会などの部屋割りに数理最適化が有用です！」と突然言われても、言葉は知っているけれど、数理最適化って部屋割りにどうやって使ったらいいんだろうと思われる方もいらっしゃると思います。なので、まずは数理最適化とは何か、何ができるのかを、先ほどの部屋割りの例に基づいて説明します。

 

数理最適化は、最適な意思決定するための数学的手法で、制約条件を満たしつつ目的関数を最大化あるいは最小化する変数の値を決めます。飲み会の部屋割りでは、各メンバーに部屋番号を割り当てる必要があるので、変数は整数で与えられる部屋番号であり、社員の人数と同じ個数あります。制約条件は、各グループの若手社員とシニア社員の割合を半々にするとか、この人とこの人は必ず同じ部屋にするなど、部屋割りの条件です。目的関数とは、部屋毎のメンバーの相性を数値化して予測して、相性の総和を最大化するとか、色々と考えられますが、ここで取り上げる例では、目的関数は考えません。

 

IBM ILOG CPLEXと IBM Decision Optimizationは、意思決定を自動化するためのソフトウェアです。最適化エンジンあるいは最適化ソルバーと呼ばれるソフトウェアです。

条件や要望が多くて悩ましい飲み会の部屋割りでも、IBM ILOG CPLEX（以下、CPLEX）あるいは IBM Decision Optimizationを利用すれば、ベストな部屋割りを行うことができます。

予測や分類は予測分析と呼ばれ主に機械学習で実現されますね。一方、予測結果から最適な意思決定を導くことは処方的分析と呼ばれ数理最適化で実現されます。

 

 

部屋割りの最適化

数理最適化とは何か、何ができるのかというところを理解したところで、CPLEXを使ってオンライン飲み会の部屋割りを行ってみましょう！

 

 

＜設定課題＞

* 本課題はCPLEX Examples – Teambuildingを参考にしています。サンプルコードはこちらです。

今回のオンライン飲み会はA, B, C, D, E, Fの６つの部署合同で開催され、各部署に所属する６０人の社員が参加します。これらの６０人の参加社員を６人ずつ１０部屋に振り分けます(情報a)。社員には0〜59の社員番号が割り振られており、新入社員は偶数、既存社員は奇数の番号が振られています(情報b)。それぞれの社員の部署は以下の通りです(情報c)。

 

部署	社員番号
A	0-19
B	20-39
C	40-44
D	45-49
E	50-54
F	55-59

 

既存社員の中には、新入社員のアドバイザーを担当している社員もいます。アドバイザーは１人の新入社員を指導しており(情報d)、それぞれの部署のアドバイザーと新入社員のペアは以下の通りです。

情報e). 部署Aでは、アドバイザー/新入社員のペアは0-1、2-3、4-5、6-7、8-9、10-11

情報f). 部署Bでは、アドバイザー/新入社員のペアは20-21、22-23、24-25、26-27、28-29、30-31.

情報g). 部署C,D,E,Fでは、アドバイザー/新入社員は40-41, 42-43, 45-46, 47-48, 50-51, 52-53, 55-56, 57-58

また、今回の飲み会は、新入社員と既存社員の親睦を深めることが目的の一つになっており、以下の５つの条件を満たすように部屋割りを行います。

 

• 制約1　１つの部屋には、既存社員３人と新入社員３人が入る。
• 制約2　同じ部署から最大４人が参加しなければならない。
• 制約3　新入社員は、その担当アドバイザーと同じ部屋でなくてはならない。
• 制約4　部署AとBの社員は同じ部屋には入れない。
• 制約5　部署EとFの社員は同じ部屋には入れない。

さらに、個別に以下のようなリクエストも挙がっています。

• 制約6　社員5は、社員41または社員51のどちらかと同じグループでなくてはならない。
• 制約7　社員15は、社員40か社員51のどちらかと同じグループでなくてはならない。
• 制約8　社員25は、社員40か社員50のどちらかと同じグループでなくてはならない。
• 制約9　社員20は社員24と同じグループか、社員22は社員50と同じグループでなくてはならない。

これら全ての条件や要望を漏れなく部屋割りに反映するのは、なかなかの労力と時間を要しそうですよね。業務の傍らの限られた時間で頑張って考えた末、最低限の条件を満たして妥協することにもなりそうです。

そんな時、数理最適化を知っていれば、妥協することなく、限られた時間内でベストな社員の組み合わせの部屋割りを提案することができるのです。

 

今回はCPLEXのPython用APIであるDOcplexライブラリを使って、Pythonスクリプトに沿って考えながら、数理最適化の威力を体験してみてください。

最初に、必要なモジュールをインポートしておきましょう。

 

---

#DOcplexインポート

from docplex.cp.model import *

---

 

さて、数理最適化のファースト・ステップは、解決したい問題を把握して現状で分かっていることを整理することです。今わかっていることは何だったかを整理しながらパラメータを設定してみましょう。

 

---

#社員60人、グループ10個を設定(情報a)

nb_persons = 60

nb_rooms = 10

teams = range(1, nb_teams+1)

#サービスA~Fを設定

serviceNames = [chr(i) for i in range(65,65+6)]

#サービスA~Fに所属するメンバーを設定(情報b, 情報c)

a = range(0,20)

b = range(20,40)

c = range(40,45)

d = range(45,50)

e = range(50,55)

f = range(55,60)

service = [set(a), set(b), set(c), set(d), set(e), set(f)]

#アドバイザー/新入社員のペア(情報d, e, f, g)

pair = namedtuple(“pair”, [“advisor”, “advised”])

pairs = [pair(0, 1), pair(2, 3), pair(4, 5), pair(6, 7), pair(8, 9), pair(10, 11),

　pair(20, 21), pair(22, 23), pair(24, 25), pair(26, 27), pair(28, 29), pair(30, 31),

　pair(40, 41), pair(42, 43), pair(45, 46), pair(47, 48), pair(50, 51), pair(52, 53), pair(55, 56), pair(57, 58)]

---

 

パラメータを設定したら、いよいよ数理最適化の最も重要なステップであるモデリング作業です。モデリングとは、決定変数と制約と目的関数をCPLEXのAPIを使ってプログラミングすることです。

 

まずは、モデルを宣言します。DOcplexではモデルを定義するためにCpoModelという関数が用意されています。今回はモデルに”teambuilding”という名前をつけました。

 

---

#モデルを定義

mdl = CpoModel(name=’teambuilding’)

---

 

次に、決定変数を定義します。決定変数は整数で与えられる部屋番号であり、社員の人数と同じ個数あります。DOcplexではinteger_var_listという関数が用意されています。サイズが参加社員の人数の60で、最小値が一番小さい部屋番号の1、最大値が一番大きい部屋番号の10の整数値をとる変数を定義します。

 

---

#決定変数を定義

team = mdl.integer_var_list(size=nb_persons, min=list(rooms)[0], max=list(rooms)[-1],  name=’person’)

---

 

さらに、制約条件を定義します。今回の問題では、与えられた５つの条件と個別に受けたリクエストの計９個の内容に当たります。数理最適化では、問題を解く上での約束事や考慮点を「制約条件」と呼びます。DOcplexでは、addやadd_constraintを用いて、制約を定義していきます。

 

---

#制約1から制約6までを設定

for t in teams:

# 1部屋の既存社員は3人（制約1）

l_existingemployee = [room[existingemployee] for existingemployee in persons if existingemployee%2==1]

mdl.add(mdl.count(l_existingemployee, t)==3)

# 1部屋の新入社員は3人（制約1）

l_newemployee = [room[newemployee] for newemployee in persons if newemployee%2==0]

mdl.add(mdl.count(l_newemployee, t)==3)

# 同じ部署から最大4人が参加（制約2）

for f in range(len(serviceNames)):

l_person = [room[person] for person in service[f]]

mdl.add(mdl.count(l_person, t)<=4)

# 部署AとBの社員は同じ部屋には入れない。(制約3)

for pA in service[serviceNames.index(‘A’)]:

for pB in service[serviceNames.index(‘B’)]:

mdl.add_constraint(room[pA] != room[pB])

# 部署EとFの社員は同じ部屋には入れない。(制約4)

for pE in service[serviceNames.index(‘E’)]:

for pF in service[serviceNames.index(‘F’)]:

mdl.add_constraint(room[pE] != room[pF])

 

# 新入社員は、その担当アドバイザーと同じ部屋でなくてはならない（制約5）

for a in pairs:

mdl.add(room[a.advisor]== room[a.advised] )

 

# 社員5は、社員41または社員51のどちらかと同じ部屋でなくてはならない（制約6）

mdl.add((room[5]== room[41]) | (room[5]== room[51]))

 

# 社員15は、社員40か社員51のどちらかと同じ部屋でなくてはならない（制約7）

mdl.add((room[15]== room[40]) | (room[15]== room[51]))

 

# 社員25は、社員40か社員50のどちらかと同じ部屋でなくてはならない（制約8）

mdl.add((room[25]== room[40]) | (room[25]== room[50]))

 

# 社員20は社員24と同じ部屋か、社員22は社員50と同じ部屋でなくてはならない(制約9)

mdl.add((room[20]== room[24]) | (room[22]== room[50]))

---

 

ここまで作成してきたモデルの情報は次のようにして確認できます。

 

---

#モデルの概要を表示

mdl.print_information()

---

 

 

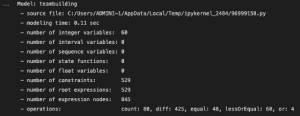
さあモデリングが完了したら、あとは解いて制約を満たすようメンバーの組み合わせを求めるだけです。DOcplexではモデルを解くのに必要な記述はとてもシンプルです。実行すると、solve関数で指定した情報と解が見つかったかどうか、消費された情報やメモリ使用量や時間などが表示されます。

 

---

#問題を解く（CPU時間を10 で制限）

msol = mdl.solve(agent=’local’,TimeLimit=10, RandomSeed=1)

---

 

 

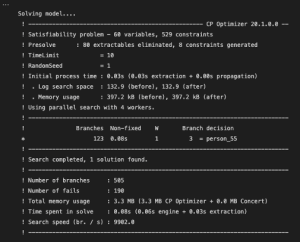
では、solveで求めた結果を表示してみまよう。求めた解はprint_solutionで表示できます。

 

---

#解を求める

msol.print_solution()

---

 

 

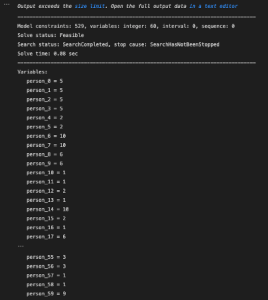
ここでは途中を省略していますが、、結果は以下の図のようになっています。

 

 

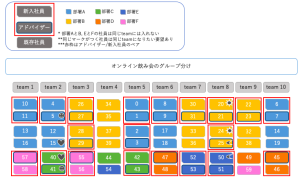
最初の<設定課題>の制約1から制約9までと照らして上図を確認してみてください。設定した制約を満たして部屋割りが行われていることが確認できます。

以上、Pythonスクリプトに沿って数理最適化について具体的に説明しました。数理最適化って便利そう、合理的に意思決定を行うのに使えそうというイメージを持っていただけたらとても嬉しいです。

 

まとめ

 

今回のオンライン飲み会の部屋割りの問題では、シンプルに制約を満たす組み合わせの問題を考えましたが、私たちの身近に、解決可能な同様の問題は溢れています。例えば学校の先生が年度はじめのクラス替えで「この子とこの子は別のクラス」という制約を設けながらクラスの学力や性別のバランスを保たないといけませんし、バイトや医療機関のスタッフ配置も当てはまります。ビジネスの領域で扱われる数理最適化もさまざまです。資源の最適配分、物流の最適化、生産スケジューリングなどがあります。

世の中には解けそうで解けない複雑な問題が数多く存在しています。そのような時に最適化問題を解くための心強いツールを知っていれば、組み合わせや調整を試行錯誤するのに費やす時間や労力を軽減でき、合理的に意思決定ができそうですね。多くの方に馴染みの深いExcelにもソルバー関数が用意されており簡単な最適化は行うことができますが、業務に関わるより大規模な問題になると、さまざまな最適化問題に対応できる高速なアルゴリズムが実装されたCPLEXが役立ちます。また、CPEXはSPSS Modelerで呼び出して使用することができ、SPSS Modelerで行った機械学習などの出力結果に最適化を組み合わせて意思決定にまでつなげることも可能です。SPSS ModelerからCPLEXを使う方法については以下の記事により詳しく書いてありますので、興味のある方はそちらもぜひ参考にしてください。

 

【リレー連載】わたしの推しノード –最強のラスボス「CPELXの最適化ノード」が予測の次の最終ステージで実力を解放

https://www.ibm.com/blogs/solutions/jp-ja/spssmodeler-push-node-19/

 

次回の身近な疑問をヒモトク#02、第２回目は気象予報士でもあるIBM西川さんが「気象データの誤解」について執筆されます。２月２１日に公開予定です。また、並行連載中のブログで学ぶSPSS Modeler#02は日本情報通信の森山さんがSQLプッシュバックを題材にしてくださいます。２月７日を予定しています。どちらもお楽しみに。

 

→IBM CLPEXの詳細についてはこちら

→SPSS Modelerの詳細についてはこちら

→これまでのTipsブログ連載のバックナンバーはこちらから

 

 

 

中島　文

日本アイ・ビー・エム株式会社

IBM Expert Labs

データサイエンティスト

 

 

 

阪本　正治（数理科学博士）

日本アイ・ビー・エム株式会社

IBM Expert Labs

データサイエンティスト