医療統計における決定木分析（ディシジョンツリー）の活用

複数の変数から、有意な要因を特定するのには時間と手間がかかります。

今回は、複数の変数から、簡単に有効な変数の発見を可能にする決定木分析（ディシジョンツリー）の利用方法について紹介します。

【前提条件】喫煙の有無について、患者データから予測を行うクロス集計とカイ2乗検定による場合

一般的な手法として知られるクロス集計とカイ2乗検定。まずはこれらの手法を利用して喫煙の有無についての分析を行ってみましょう。

性別と喫煙の関係性はあるのか？

喫煙の有無と回答者の性別のクロス表

			回答者の性別		合計
			男性	女性
喫煙の有無	はい	度数	62	80	142
		喫煙の有無の%	43.7%	56.3%	100.0%
	いいえ	度数	166	203	369
		喫煙の有無の%	45.0%	55.0%	100.0%
合計		度数	228	283	511
		喫煙の有無の%	44.6%	55.4%	100.0%

カイ2乗検定

	値	自由度	漸近有意確率（両側）	正確有意確率（両側）	正確有意確率（片側）
Pearsonカイ2乗	.073a	1	.787	.843	.433
連続修正b	.029	1	.865
尤度比	.073	1	.787
Fisherの直接法
線型と線型による連関	.073	1	.788
有効なケースの数	511

^a 0セル（.0%）は期待度数が5未満です。最小期待度数は63.36です。
^b 2×2表に対してのみ計算

• SPSS Statisticsのクロス集計の出力結果
  クロス集計の結果ならびにカイ2乗検定の結果を見る限り、性別による喫煙の比率の違いがあまり見られず、検定結果（P=0.843）からも、喫煙の有無について性別との関係はないと思われます。

続いて飲酒の経験と喫煙の有無について同様に調べてみましょう。

喫煙の有無と飲酒の経験のクロス表

			飲酒の経験		合計
			はい	いいえ
喫煙の有無	はい	度数	110	32	142
		喫煙の有無の%	77.5%	22.5%	100.0%
	いいえ	度数	243	126	369
		喫煙の有無の%	65.9%	34.1%	100.0%
合計		度数	353	158	511
		喫煙の有無の%	69.1%	30.9%	100.0%

カイ2乗検定

	値	自由度	漸近有意確率（両側）	正確有意確率（両側）	正確有意確率（片側）
Pearsonカイ2乗	6.472a	1	.011	.011	.007
連続修正b	5.940	1	.015
尤度比	6.724	1	.010
Fisherの直接法
線型と線型による連関	6.460	1	.011
有効なケースの数	511

^a 0セル（.0%）は期待度数が5未満です。最小期待度数は43.91です。
^b 2×2表に対してのみ計算

関係性は有意（P=0.011<0.05）と言えるでしょう。クロス集計表から、飲酒の経験がある人のほうが、喫煙経験がある可能性が高いと読み取ることができます。

同様に他の変数についても調べてみたいところですが、変数数が多い場合、この作業は非常に時間と手間のかかる作業となります。

また、クロス集計の適用範囲は、質的変数のみで、量的変数については利用することができません。

t検定と分散分析を利用した場合

方程式中の変数

		B	標準誤差	Wald	自由度	有意確率	Exp(B)
ステップ1a	educ	.151	.034	19.628	1	.000	1.163
	定数	-.982	.440	4.978	1	.026	.375

^a ステップ1：投入されたeduc

方程式中の変数

		B	標準誤差	Wald	自由度	有意確率	Exp(B)
ステップ1a	educ	.249	.049	26.065	1	.000	1.282
	drunk	.766	.248	9.524	1	.002	2.150
	定数	-3.693	.736	25.145	1	.000	.025

^a ステップ1：投入されたeduc,drunk
しかし、これらの手法も変数が多い場合には、1つ1つの結果を考察するのは時間と手間がかかります。

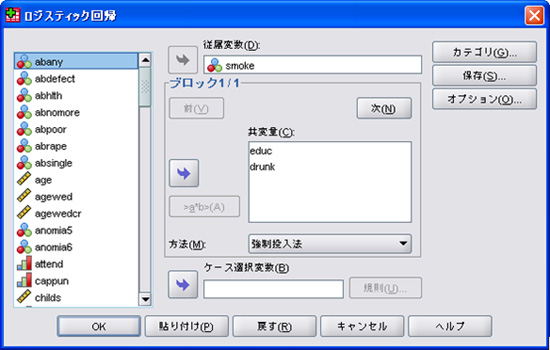
そこで、どのような独立変数が有効なのかについて調べてみたいという場合に有効なのが、決定木分析（ディシジョンツリー）です。決定木分析用のアドオンモジュールSPSS Decision Treesを利用して分析をしてみましょう。従属変数に喫煙有無を、独立変数にはその他の変数を全て投入します。

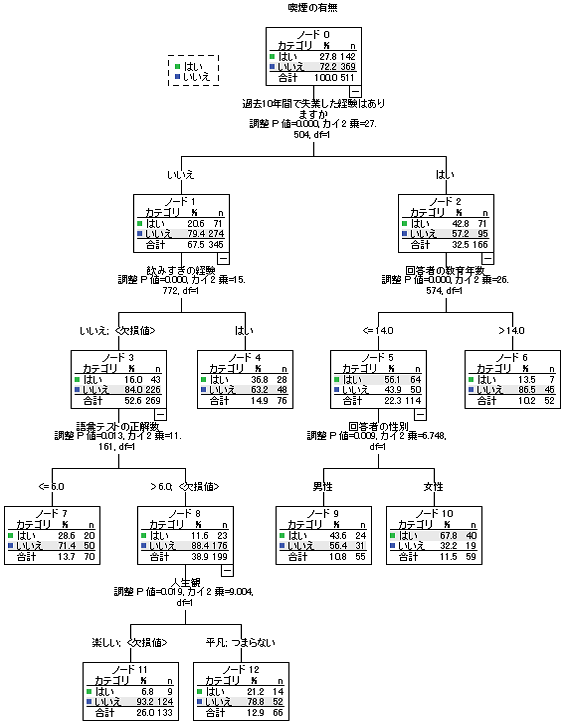
実行ボタンを押すと、右記のような図が出力されます。失業経験、教育年数、飲みすぎの経験、性別、語彙テストの結果、人生観などの変数が、喫煙の有無と関係がありそうということがひと目で理解が可能です。
このように決定木分析（ディシジョンツリー）は、非常に簡単に、そして分かりやすい分析手法です。特に交互作用（組み合わせでの差、違い）を知りたいときは有効な分析手法といえます。ぜひ決定木分析（ディシジョンツリー）をご利用ください。注意：決定木分析を利用する場合には、充分なサンプル数が必要になります。サンプル数が不足している場合には、有意な結果が出ない場合があります。また、分析手法を変えると結果にも相違が出る場合があります。（CHAID、CRT、QUEST）

• IBM SPSS Statistics：使いやすさ、解りやすさを追求した統計解析ソフトのスタンダード。統計解析ソフトSPSS Statisticsの基本ソフトウェアです。
• IBM SPSS Decision Trees：CHAID、CRT、QUESTなどを搭載する決定木分析用アドオンオプション。
• IBM SPSS Modeler：データマイニングプラットフォーム。高度な分析機能が支える独自のビジュアル・インターフェースによって、すばやくパターンと傾向をデータから発見します。