SPSS Statistics
SPSS Statistics Small Tips #04欠損値も利用!中古車販売の価格予測モデルの作成 ~ SPSS Statistics Missing Values ~
2021年11月10日
カテゴリー IBM Data and AI | SPSS Statistics | アナリティクス | データサイエンス
記事をシェアする:
欠損値、空白値を含むデータの分析
データに欠損はつきものです。どんなに完璧にシステムを作ったつもりでも抜けや漏れが生じてしまいます。特にアンケートデータには欠損が多いとされ、属性情報ですら全ての回答を得るのは難しいことも多くあります。従来、統計処理では欠損値を含むデータは分析から除外してきました。もったいない話ですが、どこかに欠損を確認すると1サンプル情報をまるごと“捨ててしまう”を行なって信頼性を優先するのが一般的でした。
しかし、実務でデータ分析をする場合、完全なデータばかりを追い求めてもいられないことが多くあります。ビジネスで使われる顧客データ、医療の現場などで使われる研究データなど様々なデータがある中、欠損値が1箇所にあるからといってデータを排除し、代わりのサンプルデータを取るとなると、非常に時間と手間、コストがかかってしまいます。また、欠損メカニズムによっては、欠損値の発生そのものに偏りがあるため、そのデータを排除することで、サンプルそのものに偏りが出てしまうという問題もあります。(例えば公平に選ばれたサンプルに対して、年収に関する質問をしたとします。ある一定以下の年収の人がその項目を答えたくないと、空欄のまま提出する傾向にあるとします。データ分析をする際そのサンプルデータは不完全だとして排除をし、全体の結果の1つとして、日本の平均年収はXXX万円です、と出たとして、果たしてその結果に偏りがないと言えるでしょうか?)
例えば商圏データを使って、店舗ごと売上予測をしたり、会員情報や購買データを使って、顧客ひとりひとりがキャンペーンに反応するかしないかを予測したいという場合があります。しかし、統計手法の性質上、予測するために使う変数=独立変数に1つでも欠損があると、予測値を算出できません。
そこで欠損値があっても“一番もっともらしい値でデータを補完することで、今あるデータを使って分析を続行できるようにする・欠損データを含むサンプルも分析対象とできるようにする”という考え方が登場し、発達してきました。それが欠損値処理、欠損値補完です。
このTipsではそんな欠損値処理のいくつかの方法について、SPSS Statisticsを使ってどのように行うのかをご紹介します。
欠損があるデータのまま予測分析をする
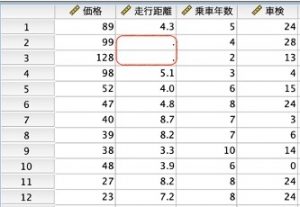
以下の例で使うデータは、Car_Missing.savで中古車12台分のデータです。データは以下から入手できます。
https://github.com/Makimaki2020/sampledata/blob/main/Car_Missing.sav?raw=true
それぞれに、中古車の価格、走行距離、乗車年数、車検の変数が数値データとして入っています。中古車の価格については、以前まではベテラン社員の方が、経験と市場価格で価格を決定していました。
しかし、この中古車ショップは走行距離、乗車年数、車検のデータを使って、中古車の価格を予測するようなモデルを作れないか?と考えました。そこで数値を予測するための回帰分析を使って、価格を予測してみることにしました。
「分析」メニュー > 「回帰」 > 「線型」 を選択し、回帰分析を行います。
価格を予測したいので、「従属変数」に『価格』を。その他の変数を「独立変数」に投入します。そして、「保存ボタン」で、予測値と残差の「標準化されていない」にチェックを入れます。これで、予測値と、予測値と実測値の差である残差がデータシートに出力されるようになります。
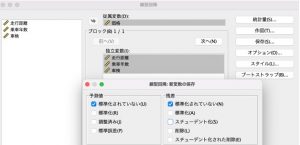
その結果PRE_1とRES_1という変数ができました。PREが予測値でRESがその残差(実測との差)になります。よい予測ができているようですが、走行距離に欠損値があるため、ケース番号2と3の中古車だけ、価格予測が計算されていません。完全なデータが揃わないと価格予測ができないということです。
これでは困ってしまいます。
しかし持っているデータでなんとか予測ができないのか?というのが実際のところではないでしょうか。ここで、欠損値処理が役に立つことになります。では実際に欠損値処理をしてみましょう。
簡単に欠損値を置換する(平均値・中央値)
はじめに、欠損値補完をしてみます。一番簡単な方法は、平均値や中央値などの統計量を当てはめ、補完する方法です。
「変換」メニュー > 「欠損値の置き換え」 を選択します。

この方法は、時系列データのような、ある一定の規則に従って、増えたり、減ったりするようなデータの補完に向いています。
まず、欠損データを含む変数を選択し、「新しい変数」に投入します。新しい変数名は、「変数名_X」のように自動で付きますが、変更も可能です。このメニューからは、補完方法として、「系列平均」、「周囲平均値」、「周囲中央値」、「線形補間」、「その点における線型トレンド」の5つから選ぶことができます。
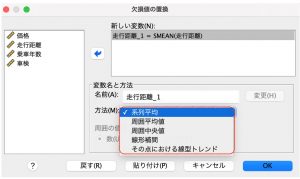
「系列平均」は、その変数の平均値を補完します。「周囲平均値」、および「周囲中央値」は、「周囲の値のスパン」で指定した数の前後のデータを使用して、中央値や平均値を算出し、欠損値を補完します。「周囲の値のスパン」が「2」の場合は、前後2つの計4つのデータを使うことになります。「線形補間」は、欠損値の前の最後の有効値および欠損値の後の最初の有効値が補間に使用されます。最初の値が1、最後の値が9だとして、ちょうど真ん中にあたるケース値が欠損していたら、その値は5になります(変数が順番に、1, ×, 9だったら、×には5が入ると予想されるという考え方です)。系列の最初のケースまたは最後のケースに欠損値がある場合、欠損値は置換されません。「その点における線型トレンド」では、1 から n に尺度化されたインデックス変数で回帰されます。欠損値はその予測値で置換されます。
これら5つの方法でも、ある程度の変数についてデータ補完ができますが、適さない変数も多いことに気づかれると思います。規則的に並んでいない場合、平均値や中央値はよいかもしれませんが、そのデータに外れ値や異常値が含まれていないことが前提になります。また、カテゴリカルデータや「はい・いいえ」などの2値データの場合はどうでしょうか?男性が多いから、欠損値には男性と入れることや、5段階評価で平均3だから無難に3を入れておくなど、統計量やデータの並び方の傾向を見ただけの処理法では欠損値をうまく予測しきれません。
欠損値には大きく3つのメカニズムがあります。1つ目はMCARと呼ばれる完全にランダムに起こってしまう欠損。2つ目はMARと呼ばれる他の変数が原因で発生している欠損(医療の現場で薬の投与の研究をしていて、患者さんが転院してしまうとそれ以上データが取れなくなって欠損してしまうという時間変数に依存する場合。また、未婚か既婚か聞く質問で女性が答えにくかったり、特定の年齢層が答えてくれなかったりするのがMARです)。3つ目はNonignorable Missing(無視できない欠損)と言い、NMARとも呼ばれますが、欠損した値に依存するというもので、非常に扱いが難しいとされています(年収の例は、欠損が年収そのものの値に依存するためNMARです)。これらのメカニズムによって、欠損値への対処法が異なります。
そこでSPSS Statisticsでは、より高度な欠損値処理を行えるよう、その他様々な手法をご用意しています。大きく分けて2つの、「単一代入法」と「多重代入法」です。次にそれら1つ1つをご紹介します。
単一代入法
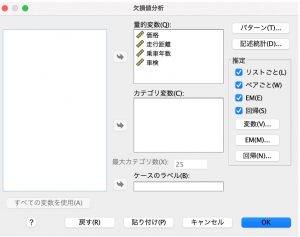
「分析」メニュー > 「欠損値分析」 を選択します。
ここでは、以下の3つを行うことができます
1.欠損データのパターンを示す
2.リストごと、ペアごと、回帰法、または EM (期待値の最大化) 法といったさまざまな欠損値手法で平均値、標準偏差、共分散、および相関を推定する。
3.回帰法または、EM法を使用して欠損値に推定値を代入する
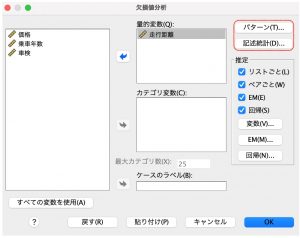
「パターン」では、次のことを調べることができます。
- 欠損値のある場所
- 変数ペアが個々のケースで値を欠損する傾向
- データ値が極値かどうか
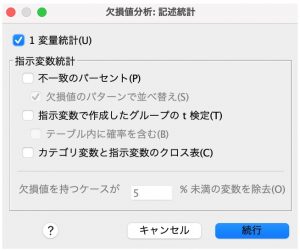
「記述統計」では、1 変量統計からは次のことがわかります。
- 非欠損値の数
- 欠損値の数とパーセント
また、量的 (スケール) 変数の場合は以下もあわせて出力されます。
- 平均値
- 標準偏差 (コレスポンデンス/ カテゴリ)
- 極大値と極小値の数
その他不一致のパーセントや、グループのt検定なども出すことが可能です。変数置換をする前に、こういった出力から傾向を掴み、適応する手法が本当に適しているのかを把握することができます。
単一代入の手法は4つあり、リストごと、ペアごと、回帰法の3つは、ランダムな欠損の場合のMCARに対応しています。
MCARは手法を選ばないため、EM法も使えます。MCARの仮定に反するMARの場合は、EM法を使用した方がよいとされています。EM法は、“欠損値のパターンは観測データのみに関連する”という仮定に依存しており、利用可能な情報を使用して推定値を調整できます。たとえば、教育と収入の調査において、教育レベルの低い被験者の方が収入の欠損値が多くなる可能性があります。つまり、収入が記録される確率が被験者の教育のレベルに依存します。この確率は、その教育レベル内の収入ではなく、教育によって異なるため、ランダムなMCARでなくMARとなります。
まず、「リストごと」・「ペアごと」で、計算に使う変数の選択方法を指定します。「リストごと」では、完全なケースのみを使用します。いずれかの分析変数に欠損値が含まれている場合、そのケースは計算から除外されます。「ペアごと」を選択すると、使用する変数ペアの1つが欠損していても、度数、平均、標準偏差は、ペアごとに個別に計算されます。
推定方法にはEM推定と回帰推定の2つがあります。EM推定を行うと、値が完全にランダムに欠損しているかどうか (MCAR) を検定するための Roderick J. A. Little のカイ 2 乗統計量が、EM 行列の脚注として出力されます。このカイ 2 乗値が 0.05 以下の場合、データは完全にランダムには欠損していないため、EM推定を使うのに適していると言えます。

「変数」ボタンでは、予測される変数と予測に使われる変数を選ぶことができます。

最後に、「EM」・「回帰」ボタンから欠損値に推定値を代入し、データシートに代入値を入れます。
その結果、回帰法、EM法それぞれの手法を使って予測された「走行距離(2,3ケース目)」に値が代入されています。
この結果、新たに得られた欠損のないデータセットで分析を続けることができます。
しかし、ここでも1つの方法だけ使い、本当にその代入が正しいのか?他の方法と比べなくてよいのか?などの単一代入法への疑問が残ります。さらに、統計や調査に詳しい方はともかく、「MCARだ、MAR、NMARだと言っても良くわからないので、とにかく一番良さそうなものを代入して欲しい」という考えもあるかもしれません。そこで、SPSS Statisticsではもう1つの手法として多重代入法を搭載しています。一般的に多重代入の方が、より正確な結果を通常生み出すと考えられています。また、ほかの手法に比べてメカニズムにこだわらず使用できます。
そもそも多重代入というのは、1つのデータ欠損に対して、複数の手法を使ってデータ補完を行うという手法です。デフォルトでは5つの手法を適応します。ここでの手法はこれまでの平均値や中央値などの基礎統計データを出すという手法は含まれません。全て、その変数だけでなく、その他の変数との関連から欠損データを予測するための手法を用いています。
まず、欠損を含むデータに対して、複数の手法を使ったデータ補完を行います。そしてそのデータに対してそれぞれにその後の分析(例えば中古車価格予測の回帰分析)などを行い、その結果を“プール”つまり統合する手法です。平均値や中央値も含め、1つの手法だけに絞り、その結果を適応していくよりも、複数のデータ補完を行った結果の平均を取るというやり方をすることで、不確実性を考慮している手法と言われています。では多重代入法をご紹介します。
多重代入法
まずは、「パターン分析」をしてみます。
「分析」メニュー > 「多重代入」 > 「パターン分析」 を選択します。
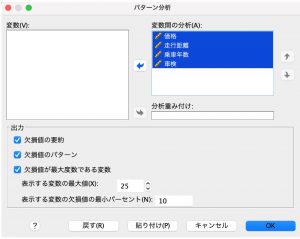

全体の要約や、変数の要約で欠損データがどれだけあるのかを確認することができます。ここでは、4つある変数のうち1つに欠損があり(「変数」)、12台の車のうち2台分(「ケース」)になります。そして、4変数X12台分の全48セル中、2つのセル(「値」)に欠損があることがわかります。その他、欠損値パターンのグラフの出力もパターン分析で見ることができます。
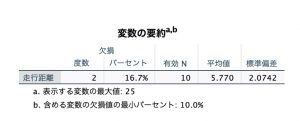
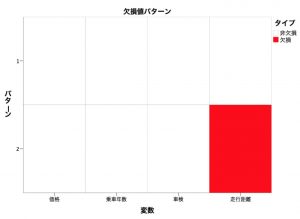
欠損値パターンのグラフから走行距離変数に欠損値があることがわかります。
ここで、欠損について把握ができたら、次に実際に値を代入してみましょう。
「分析」メニュー > 「多重代入」 > 「欠損データを代入」 を選択します。
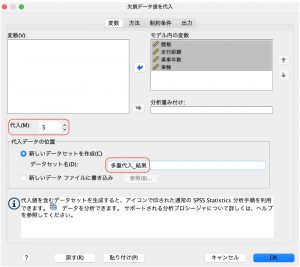
ここでも「モデル内の変数」に全ての変数を投入します。ここで変数を投入すると、欠損があるデータは欠損を埋め、欠損がないデータは欠損値を予測するために使うという指定になります。IDなどの変数以外はすべて投入して構いません。
代入されるモデルの数はデフォルトで5つです。
新しいデータセットは別ウィンドウに表示されるので、データセット名を指定します。
その他、「方法」や「制約条件」、「出力」タブで詳細の設定ができますが、ここではデフォルトのまま出力してみます。
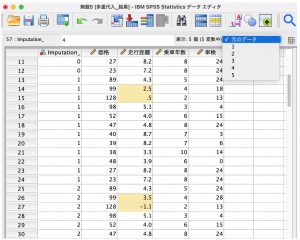
その結果、新たにデータセットが出来ます。新しい変数として、「Imputation_」という変数が出来ました。5つの手法を使って代入された結果が続いており、1から5まで付番されています。0は元データです。データのセルに色がついているところが、それぞれの代入値で、Imputationの1と2で違った値が出ています。右上のプルダウン表示を使って、それぞれのデータに移動することもできます。この時点では、5つの別の方法で代入されたデータセットができました。次にこのデータを使って、もう一度回帰分析をしてみます。
「分析」メニュー > 「回帰」 > 「線型」 を選択します。
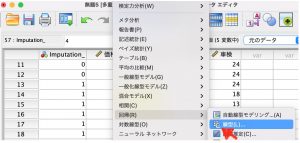
分析アイコンが変化しています。このうずまきアイコンが表示されているのが、多重代入によって得られた結果に対応している分析になります。回帰の設定は先ほどと変わりありませんので、同様に実行します。
こちらが多重代入データを使った結果のデータセットです。
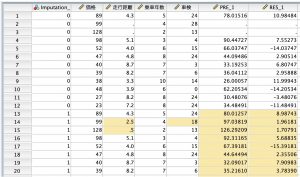
代入と代入を利用した結果は、色つきでハイライトされます。
Imputation_変数の0(元データ)では、走行距離変数のケース番号2と3のデータが欠損しており、その結果、予測値(PRE_1)と残差(RES_1)も欠損値になっています(前述と同じ結果です)。
Imputation_変数の値1~5では、走行距離の欠損値を代入しているので、予測値と残差にもデータが保存されています。
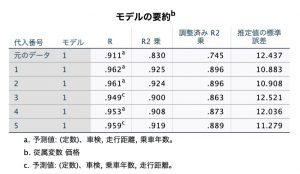
代入と代入を利用した結果は、色つきでハイライトされます。
Imputation_変数の0(元データ)では、走行距離変数のケース番号2と3のデータが欠損しており、その結果、予測値(PRE_1)と残差(RES_1)も欠損値になっています(前述と同じ結果です)。
Imputation_変数の値1~5では、走行距離の欠損値を代入しているので、予測値と残差にもデータが保存されています。
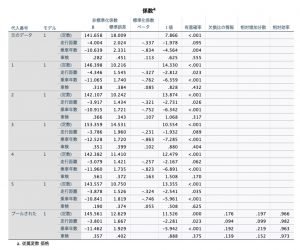
最後のモデル行に“プールされた”という結果が出ています。これが多重代入によって得られる結果です。5つのモデルで作成した値の平均を算出しています。これが、1つ1つの代入結果の不確実性を考慮した手法だと言われている所以です。多重代入で得られた結果として、この“プールされた”値を使うことができるようになります。
まとめ
このようにSPSS Statisticsでは欠損値処理に対して、様々な手法を搭載し、分析の精度をさらにアップしていただけるようになっています。特に単一代入法や、多重代入法を行うには、SPSS Statistics Missing Valuesが必要です。完全なデータではなく、欠損値があるデータでも信頼できる分析が期待できます。
さあ、さっそくはじめてみませんか。
SPSS Statistics 無料評価版 https://www.ibm.com/jp-ja/products/spss-statistics
お問い合わせは SPSS営業部まで jpsales@jp.ibm.com
→SPSS Statistics Small Tips バックナンバーはこちら

牧野 泰江
日本アイ・ビー・エム株式会社
テクノロジー事業本部 データ・AI・オートメーション事業部
Data & AI 第一テクニカルセールス
データ分析者達の教訓 #22- 予測モデルはビジネスの文脈で語られ初めてインパクトを持つ
Data Science and AI, SPSS Modeler ヒモトク, アナリティクス...
皆さんこんにちは。IBMの坂本です。 SPSSを含むデータサイエンス製品の技術を担当しています。 このリレー連載ブログはSPSS Modelerの実際のユーザーで第一線で活躍するデータ分析者に、データ活用を ...続きを読む
敷居もコストも低い! ふくろう販売管理システムがBIダッシュボード機能搭載
IBM Data and AI, IBM Partner Ecosystem
目次 販売管理システムを知名度で選んではいないか? 電子取引データの保存完全義務化の本当の意味 ふくろう販売管理システムは「JIIMA認証」取得済み AIによる売上予測機能にも選択肢を 「眠っているデータの活用」が企業の ...続きを読む
テクノロジーが向かう先とは〜中長期テクノロジー・ロードマップ
IBM Cloud Blog, IBM Data and AI
IBM テクノロジー・ビジョン・ロードマップ – IBM テクノロジー・アトラスを戦略的・技術的な予測にご活用いただけます – IBM テクノロジー・アトラスとは? IBM テクノロジー・アトラス ...続きを読む