SPSS Modeler ヒモトク
Modelerデータ加工Tips#09-IoTデータからピーク間の傾きを特徴量として抽出
2021年05月26日
カテゴリー Data Science and AI | SPSS Modeler ヒモトク | アナリティクス | データサイエンス
記事をシェアする:
みなさん、こんにちは。
現在IBMテクノロジー事業部に所属し、長年SPSS製品に携わっております牧野です。SPSS製品には、ヒモトクブログに登場するSPSS Modelerやアカデミックや医療・研究分野で多くご利用いただいているSPSS Statisticsといった主に統計解析によるデータ分析ツールがあります。どちらも多くのユーザー様にご利用いただき、ここまで成長できたことを我が子のように愛おしく思う今日このごろです。
さて、このTips#09では5/21に行われた『SPSS Modeler春のオンラインユーザー会』のプログラムに登場した「IoTデータからピーク間の傾きを特徴量として抽出する」方法について取り上げます。ユーザー会をご視聴いただきましたお客様にもまた、本ブログで初めてお読みいただくお客様にもお役立ていただければ幸いです。
具体的な手順に従って説明いたします。
例題:2つのピークの傾きを求める
行いたいことは以下の通りです。
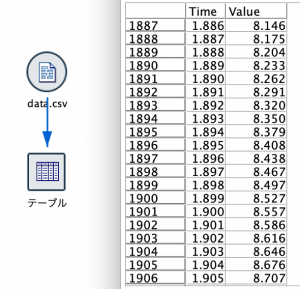
まずは、可変長ファイルノードを使ってデータを読み込みます。
例題データ
https://raw.githubusercontent.com/yoichiro0903n/blue/main/data.csv
(リンクを右クリックして「リンク先を保存」またはブラウザで開いてからページを保存します)
データをテーブルノードで表示します。以下の通り、時系列(Time)にセンサーデータ(Value)が入力されています。
データに対して、最初に行う手続きとして外せない視覚化を行います。データの可視化はデータ分析のさまざまなヒントを得るための重要なプロセスで、実際にここでも特徴量発見の手がかりとなっています。
視覚化は、データの性質に合わせて適切なグラフを選択します。今回はシーケンス(時系列)データなので、時系列グラフを作成してみます。
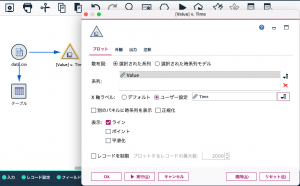
可変長ファイルノードに時系列グラフノードをリンクします。[系列]に「Value」を[X軸ラベル]を◉ユーザー設定にして、「Time」を指定します。ここでは、レコード数が4,000件程度なので、□レコードを制限の選択は解除します。
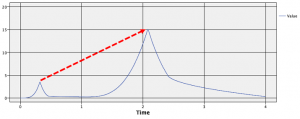
最初に登場した図と同様の2つの山があるグラフができあがりました。2つの山頂間の傾きを特徴量として試すために、それぞれの山の最大値を得る必要があります。
そこで、このグラフを使って山と山の堺に境界線を入れて2群に分けることを思いつきました。手順は以下の図の①から③の通りです。グラフを使って、データを2群に分けるフィールド作成ノードを生成します。
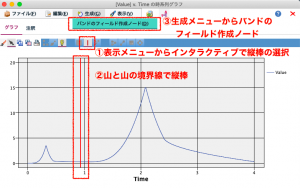
グラフからバンドのフィールド作成ノードが生成されます。これを可変長ファイルノードにリンクすれば、[値の設定条件]に基づきバンド1とバンド2にデータを分けることができます。
しかし、この方法は一時的にはよいのですが、データが変わる度にグラフを作成して、分割線を入れなくてはいけません。そのため、再現性が保てないことから汎用性のある別の方法を採用することにします。
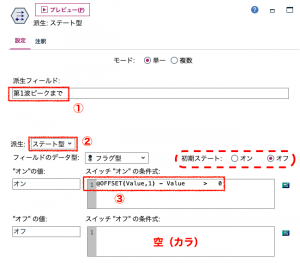
そこで、フィールド作成ノードのステート型を利用します。ステート型は2つの独立した条件を設定することができます。初期ステートで設定された状態(デフォルトは、◉オフ)から、データ値がスイッチ”オン”もしくは、スイッチ”オフ”の条件に該当した時点で、スイッチ”オン”もしくは、”オフ”のいずれかの値がデータにセットされます。結果として2種類の値を派生フィールドに返します。
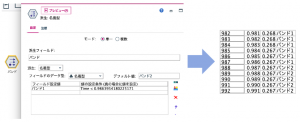
実際に設定してみます。派生フィールドに「第一波ピークまで」と入力します。[派生]を[ステート型]にします。[スイッチ”オン”の条件式]は、1つ前の値と現在の値の差を求め、その値が正(プラス)の場合とするため@OFFSET関数を使って、「@OFFSET(Value,1) – Value > 0」とします。
@OFFSET関数は、Tips#05ではJALの竹村さんが、Tips#06ではファミマデジタルワンの橋本さんも使われている通りModelerの関数の中でもトップを争うよく使う便利関数の1つですのでぜひ覚えていただくとよいと思います。
話を戻しまして、[初期ステート]は、デフォルトの◉オフです。ステート”オン”の条件は、すでに設定した通りです。また、ステート”オフ”の条件は空っぽ、つまり、条件指定をしていないので、一旦”オン”になると二度と”オフ”にはならないということになります。このステート型の使い方もちょっと異色ですよね。
フィールド作成ノードのステート型の利用に関しては、こちらの記事にも記載されています。
これで”オフ”の状態からスタートして、第一波のピークの時点で「Value」の前後の差が正(プラス)に転じて”オン”になり、それ以降”オン”をキープするというデータができあがります。
以下のようなイメージです。
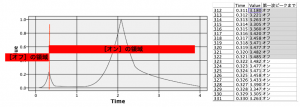
ここから【オフ】の領域のValueの最大値と【オン】の領域のValueの最大値を抽出するため、重複レコードノードを第一波ピークまでのフィールド作成ノードにリンクします。
重複レコードノードでは、[モード]を[各グループの最初のレコードだけを含める]にします。[グループ化のキーフィールド]は、「第一波ピークまで」を指定します。[並び順]の[グループ内でレコードをソート]の[フィールド]は、「Value」を指定し、[順序]を[降順]にします。
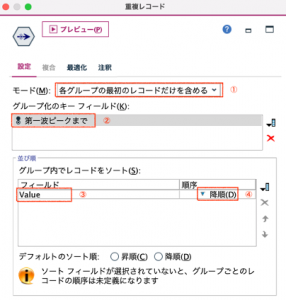
ピークが、オフとオンのそれぞれのValueの最大値を持つレコードが抽出されます。
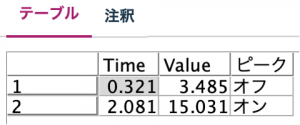
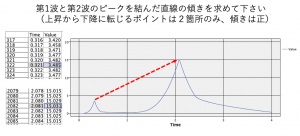
あとは傾きを求めれば良いので、Xが「Time」、Yが「Value」の2行のデータから傾きを作っていきます。それぞれXの差を分母にとってYの差を分子にとれば中学2年生で習った傾きが得られます。「Value」は、前と同じ@OFFSET関数を使って1行前の値から現在の値を引き算して分子にします。分母は同じ要領で、「Time」を使います。
重複レコードノードにフィールド作成ノードをリンクし、[派生フィールド]に「傾き」と入力します。[CLEM式]は、「(@OFFSET(Value,1) – Value) / (@OFFSET(Time,1) – Time)」とし傾きを求める式の完成です。分子と分母のそれぞれの式をかっこで括ることをお忘れなく!
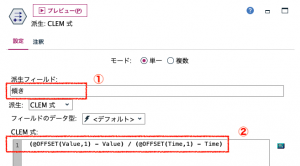
テーブルをリンクして実行します。


これで、傾きを求めることができました。
ここまでの手順は、山を分けるということをしましたが、今度は2つの山のピークを求める方法で攻めてみましょう。
データは同じですので、可変長ファイルノードにフィールド作成ノードをリンクします。そして、ここでもやはり@OFFSET関数を使用します。@OFFSETは大活躍ですね。1つ前の値と現在の値との差が負(マイナス)でかつ、現在の値と1つ後の値が正(プラス)の場合つまり、現在の値が1つ前の値より大きくかつ、1つ後の値より大きいという山の頂点に該当するレコードを見つけます。
@OFFSET関数は、現在のレコードより前(上の行)を参照する場合には、プラスの値を現在のレコードより(下の行)を参照する場合にはマイナスの値を設定します。もちろんプラス符号は省略可能です。
- @OFFSET(FIELD,5) FIELD内で5レコード前の値を参照
- @OFFSET(FIELD,-2) FIELD内で2レコード後の値を参照
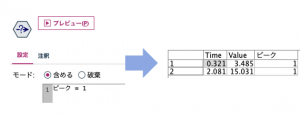
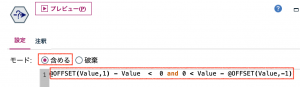
[派生フィールド]に「ピーク」と入力します。[派生]を[フラグ型]にします。[真の値]、[偽の値]はそのままでもよいのですが、今回は、[真の値]を「1」、[偽の値]を「0」にします。[真となる条件式]は、「@OFFSET(Value,1) – Value < 0 and 0 < Value – @OFFSET(Value,-1)」とします。
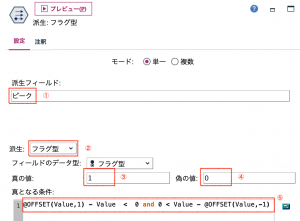
ピークが「1」のレコードを確認すると2レコード抽出され上手くいっているようです。
では、ここからさらに傾きを求めるプロセスに進みます。フィールド作成ノードをリンクします。再び@OFFSET関数を使用するのですが、実施にデータにはピークが「1」以外(ピーク「0」)のレコードがあるので、最初のピーク「1」のレコードから次のピーク「1」のレコードの差を求めるため、@SINCEと@THIS関数を使います。
@SINCEと@THISは組み合わせて使うと、同じピークフラグが立っているレコードが何行前に出てくるかを数値で返すことができます。@OFFSET関数で何行前を参照するかの数値として利用することで2つのピークの比較ができます。
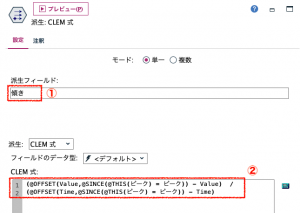
[派生フィールド]に「傾き」と入力します。[CLEM式]は、「(@OFFSET(Value,@SINCE(@THIS(ピーク) = ピーク)) – Value) / (@OFFSET(Time,@SINCE(@THIS(ピーク) = ピーク)) – Time)」とします。
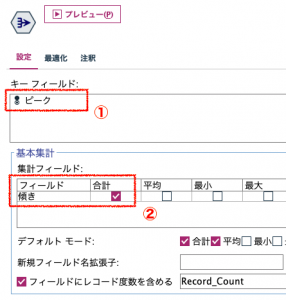
最後にピークが「1」以外のレコードは不要なので、レコード集計ノードをリンクして、[キーフィールド]に「ピーク」、[集計フィールド]に「傾き」を設定し、統計量は□合計を選択します。テーブルをリンクして実行すると傾きが確認できます。
テーブルをリンクして実行します。


レコード集計ノードを使わずに、条件抽出ノードで「ピーク = 1」を条件として◉含めるでもできますね。
実は、これまでの2つの方法のコンビネーションで、最短ストリームを作ることができます。2番目の手順にあったフィールド作成ノードのフラグ作成のための式をそのまま、条件抽出ノードの条件式として使って最初からピークの2レコードを狙い撃ちで抽出します。そして、1番目の手順の傾きを求める式を使えば、すでにピークのみの2レコードの値と時間がわかっていますので、傾きを求めることができますね。

いかがでしたでしょうか?2つのピークの傾きを求める方法をご覧いただきました。シーケンス(時系列)データに、@OFFSET関数はとてもよい仕事をします。単独でも他の関数と組み合わせても使えるシチュエーションが多数ありますね。ぜひお試しください。そして、このブログやSPSSが皆様の今後のデータ分析のお役に立てることを願っております。
Modeler詰将棋!次回のTipsから出題
次の2つの例題にチャレンジしてみてください。あいにく賞品は一切ないものの、正解すると名誉と自信がもれなくついてきます。
例題1:「予実管理テーブルを分析用に加工する」
行列入替ノードを利用したいところなのですが、対象データにヌル値があるため前後にケアをすると7手要してしまいます。行列入替を使わず5手詰め(5ノード)が最短模範例として紹介されます。フィールド名は整えなくて結構です。
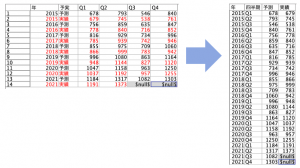
利用するデータはこちらです。
https://github.com/yoichiro0903n/blue/blob/main/forecast_before.csv
(リンクを右クリックして「リンク先を保存」またはブラウザで開いてからページを保存します)
例題2:「95%予測上限と下限を求める」
例題1の完成データから95%予測上限と下限を求めます。グラフを含めず6手詰め(6ノード)です。
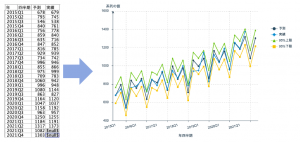
SPSS Modeler バージョン18.1以前をご利用の方はアウトプットは以下の通り。
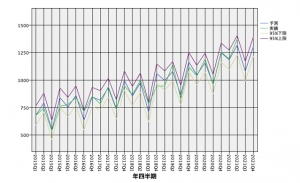
予測区間算出のロジックは以下を参考にしてください。例として示したテーブルができればグラフが描けます。
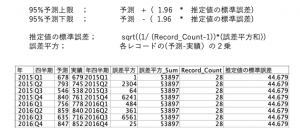
データは例題1で完成したものを利用するか、以下URLで入手ください。
https://raw.githubusercontent.com/yoichiro0903n/blue/main/forecast_after.csv
(リンクを右クリックして「リンク先を保存」またはブラウザで開いてからページを保存します)
いかがでしょうか。IBM所属のSPSS Modeler の凄腕棋士は例題1に6分、例題2には8分要したとのこと。
さて次回のTips#10はユーザー会でも登壇された東京ガスの笹谷様が解説してくださいます。
ご期待ください。

牧野 泰江
日本アイ・ビー・エム株式会社
テクノロジー事業本部 データ・AI・オートメーション事業部
Data & AI 第一テクニカルセールス
データ分析者達の教訓 #22- 予測モデルはビジネスの文脈で語られ初めてインパクトを持つ
Data Science and AI, SPSS Modeler ヒモトク, アナリティクス...
皆さんこんにちは。IBMの坂本です。 SPSSを含むデータサイエンス製品の技術を担当しています。 このリレー連載ブログはSPSS Modelerの実際のユーザーで第一線で活躍するデータ分析者に、データ活用を ...続きを読む
Women in Data Science Tokyo @ IBM 2024 開催レポート
Data Science and AI, IBM Data and AI
こんにちは。IBM西戸です。 今年で5回目のWomen in Data Science (WiDS) Tokyo @ IBM が2024年6月14日に初の会場とオンラインのハイブリッド開催されました。会場は2024年2月 ...続きを読む
法務・AIリスクのスペシャリスト三保友賀が語る「ダイバーシティー」 | インサイド・PwDA+7(後編)
Data Science and AI, IBM Sustainability Software
日本IBMにて法務、特にAI倫理・リスクのスペシャリストとして、そして同時にLGBTQ+コミュニティー*1やPwDAコミュニティー*2のアライとして積極的に活動している三保友賀さんにお話を伺いました。 前編での法務・AI ...続きを読む


